
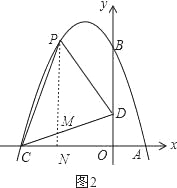
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
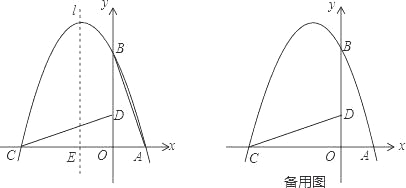
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
【答案】(1)![]()
(2)①P点的坐标为:(﹣1,4)或(﹣2,3)。
②当t=﹣![]() 时,S△PCD的最大值为
时,S△PCD的最大值为![]() 。
。
【解析】试题分析:(1)由三角函数的定义可求得OB,再结合旋转可得到A、B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)①△COD为直角三角形,可知当△CEF与△COD相似时有两种情况,即∠FEC=90°或∠EFC=90°,当PE⊥CE时,则可得抛物线的顶点满足条件,当PE⊥CD时,过P作PG⊥x轴于点G,可证△PGE∽△COD,利用相似三角形的性质可得到关于t的方程,可求得P点坐标;②可求得直线CD的解析式,过P作PN⊥x轴于点N,交CD于点M,可用t表示出PM的长,当PM取最大值时,则△PCD的面积最大,可求得其最大值.
试题解析:(1)∵OA=1.tan∠BAO=3,
∴![]() =3,解得OB=3,
=3,解得OB=3,
又由旋转可得OB=OC=3,
∴A(1,0),B(0,3),C(-3,0),
设抛物线解析式为y=ax2+bx+c,把A、B、C三点的坐标代入可得
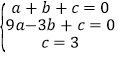 ,解得
,解得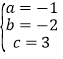 ,
,
∴抛物线解析式为y=-x2-2x+3,
(2)①由(1)可知抛物线对称轴为x=-1,顶点坐标为(-1,4),
∵△COD为直角三角形,
∴当△CEF与△COD相似时有两种情况,即∠FEC=90°或∠EFC=90°,
若∠FEC=90°,则PE⊥CE,
∵对称轴与x轴垂直,
∴此时抛物线的顶点即为满足条件的P点,此时P点坐标为(-1,4);
若∠EFC=90°,则PE⊥CD,
如图,过P作PG⊥x轴于点G,
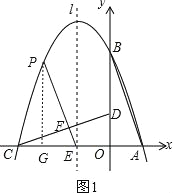
则∠GPE+∠PEG=∠DCO+∠PEG,
∴∠GPE=∠OCD,且∠PGE=∠COD=90°,
∴△PGE∽△COD,
∴![]() ,
,
∵E(-1,0),G(t,0),且P点横坐标为t,
∴GE=-1-t,PG=-t2-2t+3,
∴![]() ,解得t=-2或t=3,
,解得t=-2或t=3,
∵P点在第二象限,
∴t<0,即t=-2,
此时P点坐标为(-2,3),
综上可知满足条件的P点坐标为(-1,4)或(-2,3);
②设直线CD解析式为y=kx+m,
把C、D两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线CD解析式为y=![]() x+1,
x+1,
如图2,过P作PN⊥x轴,交x轴于点N,交直线CD于点M,
∵P点横坐标为t,
∴PN=-t2-2t+3,MN=![]() t+1,
t+1,
∵P点在第二象限,
∴P点在M点上方,
∴PM=PN-MN=-t2-2t+3-(![]() t+1)=-t2-
t+1)=-t2-![]() t+2=-(t+
t+2=-(t+![]() )2+
)2+![]() ,
,
∴当t=-![]() 时,PM有最大值,最大值为
时,PM有最大值,最大值为![]() ,
,
∵S△PCD=S△PCM+S△PDM=![]() PMCN+
PMCN+![]() PMNO=
PMNO=![]() PMOC=
PMOC=![]() PM,
PM,
∴当PM有最大值时,△PCD的面积有最大值,
∴(S△PCD)max=![]() ×
×![]() =
=![]() ,
,
综上可知存在点P使△PCD的面积最大,△PCD的面积有最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】南江县在“创国家级卫生城市”中,朝阳社区计划对某区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE,OF,OG分别是∠AOC,∠BOD,∠BOC的平分线,以下说法不正确的是( )
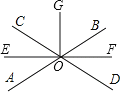
A.∠DOF与∠COG互为余角
B.∠COG与∠AOG互为补角
C.射线OE,OF不一定在同一条直线上
D.射线OE,OG互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“端午”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
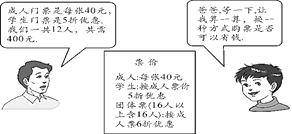
(1)他们共去了几个成人,几个学生?
(2)请你帮助算算,小明用更省钱的购票方式是指什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x<3时,y1<y2中.则正确的序号有________.

查看答案和解析>>
科目:初中数学 来源: 题型:
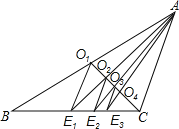
【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn= AC.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°∠ACB=60°.将Rt△ABC绕点C顺时针方向旋转后得到△DEC(△DEC≌△ABC),点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连接AD.

(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于点G,连接CG.请问:四边形ABCG是什么特殊平行四边形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(选做题)包括两个小题,请选定其中一个小题用一元一次方程作答.
A.一根尼龙绳,小江第一次用去它的一半少![]() 米,第二次用去
米,第二次用去![]() 米,结果还剩下原来的
米,结果还剩下原来的![]() ,试问这根尼龙绳原来有多长?
,试问这根尼龙绳原来有多长?
B.小苏、小江家相距![]() 千米且附近均设有火车站,一列慢车从小江家附近的火车站驶往小苏家附近的火车站,速度为
千米且附近均设有火车站,一列慢车从小江家附近的火车站驶往小苏家附近的火车站,速度为![]()
![]() ,一列快车从小苏家附近的火车站驶往小江家附近的火车站,速度为
,一列快车从小苏家附近的火车站驶往小江家附近的火车站,速度为![]()
![]() ,若两车同时出发,多少时间后两车相距
,若两车同时出发,多少时间后两车相距![]()
![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com