
【题目】如图,开口向下的抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是第一象限内抛物线上的一点.
是第一象限内抛物线上的一点.
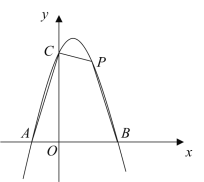
(1)求该抛物线所对应的函数解析式;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
科目:初中数学 来源: 题型:
【题目】某百货公司进了一批商品,进货价为20元/件,有专家预计月销量![]() (件)关于售价
(件)关于售价![]() (元/件)的函数解析式为
(元/件)的函数解析式为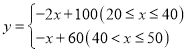
(1)若百货公司销售该商品月利润为![]() 元,写出
元,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)当售价![]() 为多少时,百货公司销售该商品的月利润最大,最大月利润是多少?
为多少时,百货公司销售该商品的月利润最大,最大月利润是多少?
(3)当百货公司销售该商品的月利润不少于400元时,试确定商品的售价![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,BC=4![]() ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
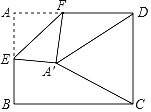
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的表达式及对称轴;
(2)点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
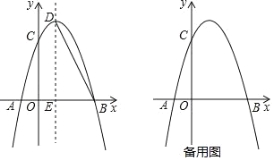
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM =![]() 海里,那么该船继续航行______海里可使渔船到达离灯塔距离最近的位置.
海里,那么该船继续航行______海里可使渔船到达离灯塔距离最近的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
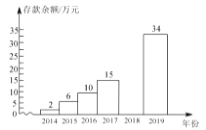
【题目】小李2014年参加工作,每年年底都把本年度收入减去支出后的余额存入银行(存款利息记入收入),2014年底到2019年底,小李的银行存款余额变化情况如下表所示:(单位:万元)
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
收入 | 3 | 8 | 9 |
| 14 | 18 |
支出 | 1 | 4 | 5 | 6 |
| 6 |
存款余额 | 2 | 6 | 10 | 15 |
| 34 |
(1)表格中![]() ________;
________;
(2)请把下面的条形统计图补充完整:(画图后标注相应的数据)
(3)请问小李在哪一年的支出最多?支出了多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com