
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中, ,
,
∴△DAP≌△ABQ,
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP;
故①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴![]() ,
,
∴AO2=ODOP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OEOP;故②错误;
在△CQF与△BPE中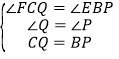 ,
,
∴△CQF≌△BPE,
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中, ,
,
∴△ADF≌△DCE,
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故③正确;
∵BP=1,AB=3,
∴AP=4,
∵△AOP∽△DAP,
∴![]() ,
,
∴BE=![]() ,∴QE=
,∴QE=![]() ,
,
∵△QOE∽△PAD,
∴![]() ,
,
∴QO=![]() ,OE=
,OE=![]() ,
,
∴AO=5﹣QO=![]() ,
,
∴tan∠OAE=![]() =
=![]() ,故④正确,
,故④正确,
故选C.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图(1), 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B、C在A、E的异侧, BD⊥AE于D, CE⊥AE于E

(1)试说明: BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD与DE、CE的关系如何? 为什么?

(3)若直线AE绕A点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD与DE、CE的关系如何? 请 直接写出结果, 不需说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁在网格(每小格边长为1)上沿着网格线运动.它从格点![]() 处出发去看望格点B、C、D等处的蚂蚁,规定:向上向右走均为正,向下向左走均为负.如:从A到B记为:
处出发去看望格点B、C、D等处的蚂蚁,规定:向上向右走均为正,向下向左走均为负.如:从A到B记为:![]() ,从B到A记为:
,从B到A记为:![]() ,其中第一个数表示左右方向,第二个数表示上下方向.
,其中第一个数表示左右方向,第二个数表示上下方向.

(1)填空:图中![]() ,
,![]() ;
;
(2)若这只蚂蚁从A处去M处的蚂蚁的行走路线依次为![]() ,
,![]() ,
,![]() ,
,![]() ,则点M的坐标为(________,________);
,则点M的坐标为(________,________);
(3)若图中另有两个格点Р、Q,且![]() ,
,![]() ,则从Q到A记为________________.
,则从Q到A记为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C'处,BC'交AD于点E.

(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,AD=8,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明AP=AQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,点D在斜边AB上,且AD=AC,过点B作BE⊥CD,交直线CD于点E.
(1)求∠BCD的度数;
(2)作AF⊥CD于点F,求证:△AFD≌△CEB;
(3)请直接写出CD与BE的数量关系(不需要证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 交
交![]() 于
于![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 交
交![]() 的延长线于
的延长线于![]() ,
,![]() 的延长线交
的延长线交![]() 于
于![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() ;②∠AGH=∠BAE+∠ACB;③
;②∠AGH=∠BAE+∠ACB;③![]() ,其中正确的结论有( )个.
,其中正确的结论有( )个.

A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD是一张矩形纸片,AB=3cm,BC=5cm

(1)在矩形ABCD的边AD上找一点E,使CE平分∠BED,请利用刻度尺或圆规作出点E,写出作法,并给出证明;
(2)把矩形纸片沿某直线剪一刀分成两部分后,再用这两部分拼成一个菱形,请画出剪拼的示意图,并求出菱形的较长对角线的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com