
【题目】已知:四边形ABCD是一张矩形纸片,AB=3cm,BC=5cm

(1)在矩形ABCD的边AD上找一点E,使CE平分∠BED,请利用刻度尺或圆规作出点E,写出作法,并给出证明;
(2)把矩形纸片沿某直线剪一刀分成两部分后,再用这两部分拼成一个菱形,请画出剪拼的示意图,并求出菱形的较长对角线的长度.
【答案】(1)见解析;(2)见解析,![]()
【解析】
(1)如图1,利用“倒推法”,要作CE平分∠BED,就要∠BEC=∠DEC,而∠BCE=∠DEC,那么∠BCE=∠BEC,即BC=BE,只要作出BC=BE即可;
(2)如图2所示,沿BE裁剪,将△ABE平移至△DCF位置,由(1)知:四边形BCFE四边都相等,则四边形BCFE即为所求;在Rt△ABE中可求得AE的长,Rt△ABF中就可以求得AF的长,利用勾股定理可求得答案.
解:(1)如图1所示,点E即为所求;
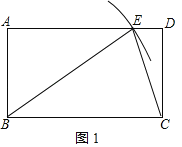
由作图知BC=BE,
∴∠BCE=∠BEC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BCE=∠DEC,
∴∠BEC=∠DEC,
∴EC平分∠BED;
(2)如图2所示,沿BE裁剪,将△ABE平移至△DCF位置,则四边形BCFE即为所求,
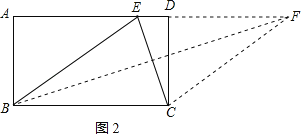
由(1)知:BC=BE=5,
∵AB=3,∠A=90°,
∴DF=AE=![]() =4,
=4,
则AF=AD+DF=5+4=9,
∴BF=![]() =3
=3![]() (cm).
(cm).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(实验操作)如图①,在![]() 中,
中,![]() ,现将
,现将![]() 边沿
边沿![]() 的平分线
的平分线![]() 翻折,点
翻折,点![]() 落在
落在![]() 边的点
边的点![]() 处;再将线段
处;再将线段![]() 沿
沿![]() 翻折到线段
翻折到线段![]() ,连接
,连接![]() .
.
(探究发现)若点![]() ,
,![]() ,
,![]() 三点共线,则
三点共线,则![]() 的大小是______,
的大小是______,![]() 的大小是________,此时三条线段
的大小是________,此时三条线段![]() ,
,![]() ,
,![]() 之间的数量关系是________.
之间的数量关系是________.
(应用拓展)如图②,将图①中满足(实验操作)与(探究发现)的![]() 的边
的边![]() 延长至
延长至![]() ,使得
,使得![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的度数.
的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
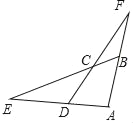
【题目】如图,已知四边形ABCD的一组对边AD、BC的延长线相交于点E.另一组对边AB、DC的延长线相交于点F,若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是 “书”的概率为__________.
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.


备用图
(1)![]() ___________
___________![]() ;
;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值:
的值:
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com