
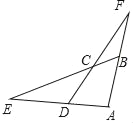
【题目】如图,已知四边形ABCD的一组对边AD、BC的延长线相交于点E.另一组对边AB、DC的延长线相交于点F,若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
【答案】![]()
【解析】分析:作辅助线,构建直角三角形,利用三角函数计算DH和CH的长,并设AD=5a,则DG=3a,AG=4a,证明△AFG∽△CEH,列比例式可得a的值,从而得AD的长.
详解:过C作CH⊥AD于H.
∵cos∠ADC=![]() ,CD=5,∴DH=3,∴CH=4,∴tan∠E=
,CD=5,∴DH=3,∴CH=4,∴tan∠E=![]() =
=![]() ,
,
过A作AG⊥CD于G,设AD=5a,则DG=3a,AG=4a,
∴FG=DF﹣DG=5+n﹣3a.
∵CH⊥AD,AG⊥DF.
∵∠CHE=∠AGF=90°.
∵∠ADC=∠ABC,∴∠EDC=∠CBF.
∵∠DCE=∠BCF,∴∠E=∠F,∴△AFG∽△CEH,
∴![]() ,∴a=
,∴a=![]() ,∴AD=5a=
,∴AD=5a=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=![]() ,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )
,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )

A. 2 ![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD 和△BCE ,连接AE,CD与GF,下列结论正确的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
(1)若PD⊥AB,求AP.
(2)当AD=PE时,求证:四边形BDEP为菱形.
(3)若△PDE与△ABC重合部分的面积等于△PAB面积的![]() ,求AP.
,求AP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花果山上有两只猴子在一棵树CD上的点B处,且BC=5m,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树10m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处.已知两只猴子所经过的路程相等,设BD为xm.
(1)请用含有x的整式表示线段AD的长为______m;
(2)求这棵树高有多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形ABCD中,AB=5,AD=12,E为AD边上一点,DE=4,动点P从点B出发,沿B→C→D以2个单位/s作匀速运动,设运动时间为t.
⑴ 当t为 s时,△ABP与△CDE全等;
⑵ 如图2,EF为△AEP的高,当点P在BC边上运动时,EF的最小值是 ;
⑶ 当点P在EC的垂直平分线上时,求出t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com