
【题目】在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
(1)若PD⊥AB,求AP.
(2)当AD=PE时,求证:四边形BDEP为菱形.
(3)若△PDE与△ABC重合部分的面积等于△PAB面积的![]() ,求AP.
,求AP.

【答案】(1)![]() ;(2)见解析:(3) AP=3或
;(2)见解析:(3) AP=3或![]() .
.
【解析】
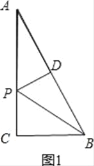
(1)如图1,根据勾股定理可求出AB,从而得到AD、BD的值,易证△ADP∽△ACB,只需运用相似三角形的性质就可求出AP的值;
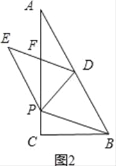
(2)由折叠可得:PE=PB,DE=DB,又有AD=PE,AD=DB,从而PE=PB=DB=DE,然后根据四条边相等的四边形形是菱形即可证明四边形BDEP为菱形;
(3)根据条件可得S△PDF=![]() S△PAB=
S△PAB=![]() S△ADP=
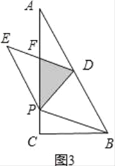
S△ADP=![]() S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=2
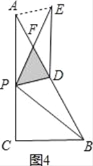
S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=2![]() ,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=2
,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=2![]() .
.
解:(1)如图1,
∵∠C=90°,BC=2,AC=4,
∴AB=![]() =2
=2![]() .
.
∵点D为AB的中点,
∴AD=BD=![]() .
.
∵PD⊥AB,
∴∠ADP=90°.
∵∠A=∠A,∠ADP=∠C,
∴△ADP∽△ACB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AP=![]() ;
;
(2)证明:如图2,
由折叠可得:PE=PB,DE=DB.
∵AD=PE,AD=DB,
∴PE=PB=DB=DE,
∴四边形BDEP为菱形;
(3)∵点D是线段AB的中点,
∴S△ADP=S△BDP=![]() S△PAB.
S△PAB.
由折叠可得:S△EDP=S△BDP,
∴S△PDF=![]() S△PAB=
S△PAB=![]() S△ADP=
S△ADP=![]() S△EDP,
S△EDP,
∴AF=PF,EF=DF.
①如图3,
根据三角形中位线定理可得:DF∥BP,
∴∠EDP=∠BPD.
由折叠可得∠BDP=∠EDP,
∴∠BDP=∠BPD,
∴BP=BD=![]() ,
,
∴PC=![]() =
=![]() =1,
=1,
∴AP=4﹣1=3;
②如图4,
连接AE,
∵AF=DF,EF=PF,
∴四边形AEDP是平行四边形,
∴AP=ED,
由折叠可得:DE=DB,
∴AP=DB=![]() .
.
综上所述:AP=3或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点均在格点上,请按要求完成下列各题:
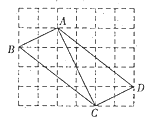
(1)线段AC的长为________,CD的长为________,AD的长为________.
(2)试判断![]() 的形状并求出四边形ABCD的面积.
的形状并求出四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )

A. △ABC中,AD是边BC上的高
B. △ABC中,GC是边BC上的高
C. △GBC中,GC是边BC上的高
D. △GBC中,CF是边BG上的高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,已知A(0,4),B(﹣2,2),C(3,0).

(1)在如图网格中画出△ABC,及△ABC关于x轴对称的△A1B1C1;
(2)写出点A1、B1、C1的坐标.
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

查看答案和解析>>
科目:初中数学 来源: 题型:
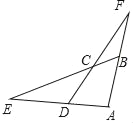
【题目】如图,已知四边形ABCD的一组对边AD、BC的延长线相交于点E.另一组对边AB、DC的延长线相交于点F,若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图四边形OACB是菱形,OB在X轴的正半轴上,sin∠AOB=![]() .反比例函数y=
.反比例函数y=![]() 在第一象限图象经过点A,与BC交于点F.S△AOF=
在第一象限图象经过点A,与BC交于点F.S△AOF=![]() ,则k=( )
,则k=( )

A. 15 B. 13 C. 12 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
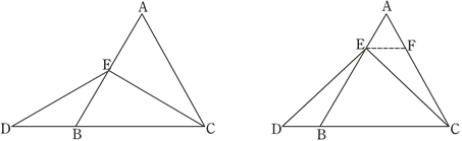
图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com