
【题目】已知:如图四边形OACB是菱形,OB在X轴的正半轴上,sin∠AOB=![]() .反比例函数y=
.反比例函数y=![]() 在第一象限图象经过点A,与BC交于点F.S△AOF=
在第一象限图象经过点A,与BC交于点F.S△AOF=![]() ,则k=( )
,则k=( )

A. 15 B. 13 C. 12 D. 5
【答案】A
【解析】
过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,再根据四边形OACB是菱形、点F在边BC上,即可得出S△AOF=S菱形OBCA,结合菱形的面积公式即可得出a的值,进而依据点A的坐标得到k的值.
过点A作AM⊥x轴于点M,如图所示.
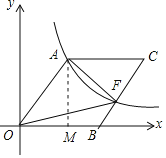
设OA=a=OB,则,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=![]() ,
,
∴AM=OAsin∠AOB=![]() a,OM=
a,OM=![]() a,
a,
∴点A的坐标为(![]() a,
a,![]() a).
a).
∵四边形OACB是菱形,S△AOF=![]() ,
,
∴![]() OB×AM=
OB×AM=![]() ,
,
即![]() ×a×
×a×![]() a=39,
a=39,
解得a=±![]() ,而a>0,
,而a>0,
∴a=![]() ,即A(
,即A(![]() ,6),
,6),
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴k=![]() ×6=15.
×6=15.
故选A.
【解答】
解:


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两人沿同一条路从
,甲、乙两人沿同一条路从![]() 地到
地到![]() 地.
地.![]() ,
,![]() 分别表示甲、乙两人离开
分别表示甲、乙两人离开![]() 地的距离
地的距离![]() 与时间
与时间![]() 之间的关系.
之间的关系.
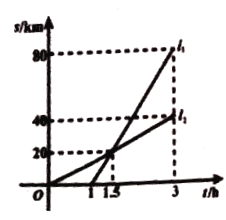
(1)乙先出发________![]() 后,甲才出发;直接写出
后,甲才出发;直接写出![]() ,
,![]() 的表达式.
的表达式.
(2)甲到达![]() 地时,乙还需几小时到达
地时,乙还需几小时到达![]() 地?
地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
(1)若PD⊥AB,求AP.
(2)当AD=PE时,求证:四边形BDEP为菱形.
(3)若△PDE与△ABC重合部分的面积等于△PAB面积的![]() ,求AP.
,求AP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花果山上有两只猴子在一棵树CD上的点B处,且BC=5m,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树10m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处.已知两只猴子所经过的路程相等,设BD为xm.
(1)请用含有x的整式表示线段AD的长为______m;
(2)求这棵树高有多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.

(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一张五边形的钢板ABCDE如图所示,∠A=∠B=∠C=90°,现在AB边上取一点P,分别以AP,BP为边各剪下一个正方形钢板模型,所剪得的两个正方形面积和的最大值为_____m2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com