
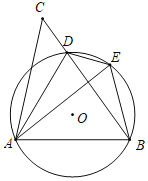
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在⊙O上.
(1)求证:AE=AB.
(2)填空:
①当∠CAB=90°,cos∠ADB=![]() ,BE=2时,边BC的长为 .
,BE=2时,边BC的长为 .
②当∠BAE= 时,四边形AOED是菱形.
【答案】(1)见解析;(2)①3![]() ;②60°
;②60°
【解析】
(1)利用折叠的性质得出AC=AE,∠C=∠AED,再判断出∠C=∠ABC,得出AB=AC,即可得出结论;
(2)①先求出EF=1,再判断出∠AEB=∠ADB,利用锐角三角函数求出AE,进而求出AB,即可得出结论;
②先判断出△AOD是等边三角形,得出∠ADO=60°,进而求出∠ADE=120°,再求出∠C=∠ABC=∠DAC=30°,即可求出∠BAC=120°,利用折叠的性质求出∠CAE=60°,即可得出结论.
(1)证明:由折叠知,AC=AE,∠C=∠AED,
∵∠ABC=∠AED,
∴∠C=∠ABC,
∴AB=AC,
∴AE=AB;
(2)①如图1,过点A作AF⊥BE于F,
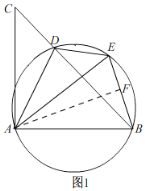
由(1)知,AE=AB,
∴EF=![]() BE=1,
BE=1,
∵∠ADB=∠AEB,cos∠ADB=![]() ,
,
∴cos∠AEB=![]() ,
,
在Rt△AFE中,cos∠AEB=![]() =
=![]() ,
,
∴AE=3EF=3,
由(1)知,AE=AB,
∴AB=3,
由(1)知,AB=AC,
∵∠CAB=90°,
∴BC=![]() AB=3
AB=3![]() ,
,
故答案为3![]() ;
;
②如图2,
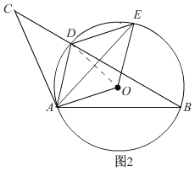
∵四边形AOED是菱形,
∴DE=OA=AD,
连接OD,
∴OA=OD,
∴AD=OA=OD,
∴△AOD是等边三角形,
∴∠ADO=60°,
同理:∠ODE=60°,
∴∠ADE=∠ADO+∠ODE=120°,
由折叠知,CD=DE,∠ADC=∠ADE,
∴∠ADC=120°,
∵AD=DE,
∴CD=AD,
∴∠DAC=∠C=![]() (180°﹣∠ADC)=30°,
(180°﹣∠ADC)=30°,
由(1)知,∠ABC=∠C,
∴∠BAC=180°﹣∠C﹣∠ABC=120°,
由折叠知,∠DAE=∠DAC=30°,
∴∠CAE=∠DAC+∠DAE=60°,
∴∠BAE=∠BAC﹣∠CAE=60°,
故答案为60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
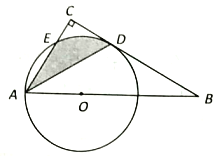
【题目】如图,点0 为Rt△ABC斜边AB上的一点,以OA 为半径的☉O与BC切于点D,与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的顶点
的顶点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点.
的交点.
(1)用含![]() 的代数式表示顶点
的代数式表示顶点![]() 的坐标.
的坐标.
(2)①当![]() 时,
时,![]() 的值均随
的值均随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
②若![]() ,且
,且![]() 满足
满足![]() 时,二次函数的最小值为
时,二次函数的最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)试证明:无论![]() 取任何值,二次函数
取任何值,二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点.
总有两个不同的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
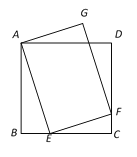
【题目】如图,已知正方形ABCD中,点E是BC上的一个动点,EF⊥AE交CD于点F,以AE,EF为边作矩形AEFG,若AB=4,则点G到AD距离的最大值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备购进一批产品进行销售,该产品的进货单价为6元/个.根据市场调查,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.关于日销售量y(个)与销售单价x(元/个)的几组数据如表:
x | 10 | 12 | 14 | 16 |
y | 300 | 240 | 180 | m |
(1)求出y与x之间的函数关系式(不要求写出自变量的取值范围)及m的值.
(2)按照(1)中的销售规律,当销售单价定为17.5元/个时,日销售量为 个,此时,获得日销售利润是 .
(3)为防范风险,该公司将日进货成本控制在900(含900元)以内,按照(1)中的销售规律,要使日销售利润最大,则销售单价应定为多少?并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB= ![]() ,BC=1,连结BF,分别交AC、DC、DE于点P、Q、R.
,BC=1,连结BF,分别交AC、DC、DE于点P、Q、R.
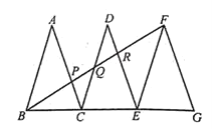
(1)求证:△BFG∽△FEG
(2)求sin∠FBG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
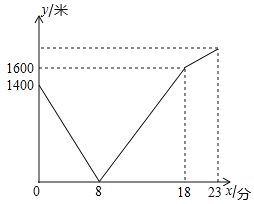
【题目】小婷家与学校之间是一条笔直的公路,小婷从家步行前往学校的途中发现忘记带昨天的回家作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小婷沿原路返回![]() 两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
![]() 妈妈从家出发______分钟后与小婷相遇;
妈妈从家出发______分钟后与小婷相遇;
![]() 相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米
相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com