
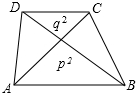
 如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.
如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2. 分析 过O作OE⊥CD于E,延长EO交AB于F,则EF为梯形ABCD的高,根据△COD和△AOB的面积可以求得AB、CD的值,根据AB、CD、EF的值即可计算梯形ABCD的面积,即可解题.
解答 解:∵四边形ABCD是梯形,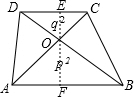
∴AB∥CD,
如图,过O作OE⊥CD于E,延长EO交AB于F,
则EF⊥AB,
∴△ABO∽△CDO,
∴$\frac{CD}{AB}=\frac{OE}{OF}=\sqrt{\frac{{S}_{△CDO}}{{S}_{△ABO}}}$=q:p,
设上下底分别为mq,mp,两个三角形对应的高分别为nq,np,
有$\frac{mp•np}{2}$=p2,得mn=2
∴S梯形ABCD=$\frac{(mp+mq)(np+nq)}{2}$=$\frac{mn(p+q)^{2}}{2}$=(p+q)2,
故答案为:(p+q)2.
点评 本题考查了相似三角形的判定和性质,梯形面积的计算,考查了直角三角形中勾股定理的运用,本题中求EF的值是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 111 | B. | 118 | C. | 125 | D. | 132 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3900(1+x)2=2500 | B. | 3900(1-x)2=2500 | C. | 3900(1-2x)=2500 | D. | 2500(1+x)2=3900 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(x+2y)(x-2y) | B. | a(x-2y)2 | C. | a(x-4y)2 | D. | a(x+4y)(x-4y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
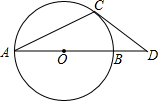 如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=$\sqrt{2}$-1,则∠ACD=112.5°.
如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=$\sqrt{2}$-1,则∠ACD=112.5°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com