
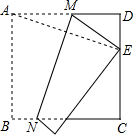
 如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为( )
如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为( )| A. | 10 | B. | 13 | C. | 15 | D. | 无法求出 |
分析 根据图形折叠前后图形不发生大小变化可得出∠DAE=∠DAE,再证明△NFM≌△ADE,然后利用勾股定理的知识求出MN的长.
解答 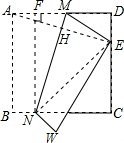 解:作NF⊥AD,垂足为F,连接AE,NE,
解:作NF⊥AD,垂足为F,连接AE,NE,
∵将正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,
∴∠D=∠AHM=90°,∠DAE=∠DAE.
∴△AHM∽△ADE.
∴∠AMN=∠AED.
在Rt△NFM和Rt△ADE中,
$\left\{\begin{array}{l}{∠AMN=∠AED}\\{∠NFM=∠D}\\{AD=NF}\end{array}\right.$,
∴△NFM≌△ADE(AAS),
∴FM=DE=CD-CE=5cm,
又∵在Rt△MNF中,FN=AB=12cm,
∴根据勾股定理得:MN=$\sqrt{F{N}^{2}+F{M}^{2}}$=13.
故选B.
点评 此题主要考查了图形的翻折变换,根据图形折叠前后图形不发生大小变化得出三角形的全等是解决问题的关键,难度一般.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:解答题
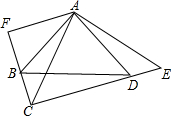 如图,△ABD和△ACE均为等腰直角三角形,A为公共直角顶点,过A作AF垂直CB交CB的延长线于F.
如图,△ABD和△ACE均为等腰直角三角形,A为公共直角顶点,过A作AF垂直CB交CB的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线AB与x轴、y轴的正半轴分别交于点A,B,直线CD与x轴正半轴、y轴负半轴分别交于点D,C,AB与CD相交于点E,点A,B,C,D的坐标分别为(8,0)、(0,6)、(0,-3)、(4,0),点M是OB的中点,点P在直线AB上,过点P作PQ∥y轴,交直线CD于点Q,设点P的横坐标为m.
如图,在平面直角坐标系中,直线AB与x轴、y轴的正半轴分别交于点A,B,直线CD与x轴正半轴、y轴负半轴分别交于点D,C,AB与CD相交于点E,点A,B,C,D的坐标分别为(8,0)、(0,6)、(0,-3)、(4,0),点M是OB的中点,点P在直线AB上,过点P作PQ∥y轴,交直线CD于点Q,设点P的横坐标为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com