【题目】某路公交车起点站设在一居民小区附近，为了解高峰时段从该起点站乘车出行的人数，随机抽查了高峰时段10个班次从该起点站乘车的人数，结果如下：20、23、26、25、29、28、30、25、21、23.如果在高峰时段从该起点站共发车60个班次，那么估计在高峰时段从该起点站乘该路车出行的乘客一共有________人.
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案科目：初中数学 来源： 题型：
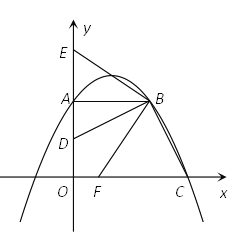
【题目】如图，已知直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA＝AB＝2，OC＝3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于E和F．
（1）求经过A、B、C三点的抛物线的解析式；
（2）当BE经过（1）中抛物线的顶点时，求CF的长；
（3）连结EF，设△BEF与△BFC的面积之差为S，问：当CF为何值时S最小，并求出这个最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设p,q都是实数,且p<q.我们规定:满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间,表示为[p,q].对于一个函数,如果它的自变量x与函数值y满足:当p≤x≤q时,有p≤y≤q,我们就称此函数是闭区间[p,q]上的“闭函数”.反比例函数y=
是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
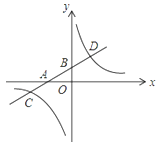
【题目】如图，在平面直角坐标系中，一次函数y=kx+b的图象分别交x轴、y轴于A、B两点，与反比例函数y=
的图象交于C、D两点，DE⊥x轴于点E，已知C点的坐标是（﹣6，﹣1），DE=3．
（1）求反比例函数与一次函数的解析式．
（2）根据图象直接回答：当x为何值时，一次函数的值小于反比例函数的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟．在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t
（分）之间的关系如图所示，下列结论：
①甲步行的速度为60米/分；
②乙走完全程用了30分钟；
③乙用16分钟追上甲；
④乙到达终点时，甲离终点还有320米
其中正确的结论有（ ）
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知△ABC顶点坐标分别为A(0，3)，B(1，1)，C(﹣3，﹣1)，△DEF与△ABC关于y轴对称，且A，B，C依次对应D，E，F，
(1)请写出D，E，F的坐标.
(2)在平面直角坐标系中画出△ABC和△DEF.
(3)经过计算△DEF各边长度，发现DE、EF、FD满足什么关系式，写出关系式.
(4)求△DEF的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某农户承包荒山种了44棵苹果树．现在进入第三年收获期．收获时，先随意摘了5棵树上的苹果，称得每棵树摘得的苹果重量如下（单位：千克）35 35 34 39 37
(1)在这个问题中，总体指的是？个体指的是？样本是？样本容量是？
(2)试根据样本平均数去估计总体情况，你认为该农户可收获苹果大约多少千克？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有两条互相垂直的公路
，A厂离公路
的距离为2千米，离公路
的距离为5千米；B厂离公路的距离为11千米，离公路的距离为4千米；现在要在公路上建造一仓库P，使A厂到P仓库的距离与B厂到P仓库的距离相等，求仓库P的位置．
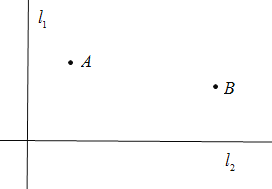
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】九年级学生到距离学校6千米的百花公园去春游，一部分学生步行前往，20分钟后另一部分学生骑自行车前往，设
（分钟）为步行前往的学生离开学校所走的时间，步行学生走的路程为
千米，骑自行车学生骑行的路程为
千米，
关于的函数图象如图所示.
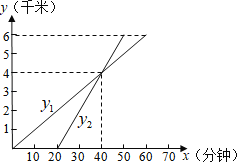
（1）求关于的函数解析式；
（2）步行的学生和骑自行车的学生谁先到达百花公园，先到了几分钟？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
