
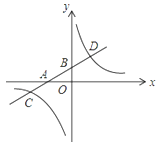
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y=![]() 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(﹣6,﹣1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(﹣6,﹣1),DE=3.
(1)求反比例函数与一次函数的解析式.
(2)根据图象直接回答:当x为何值时,一次函数的值小于反比例函数的值.
【答案】(1) y=![]() x+2;(2) 当x<﹣6或0<x<2时,一次函数的值小于反比例函数的值
x+2;(2) 当x<﹣6或0<x<2时,一次函数的值小于反比例函数的值
【解析】
(1)先由点C的坐标求出反比例函数的关系式,再由DE=3,求出点D的坐标,把点C,点D的坐标代入一次函数关系式求出k,b即可求一次函数的关系式;
(2)由图象可知:一次函数的值小于反比例函数的值的时候x的取值范围.
(1)点C(﹣6,﹣1)在反比例函数y=![]() 的图象上,
的图象上,
∴m=﹣6×(﹣1)=6,
∴反比例函数的关系式为y=![]() ,
,
∵点D在反比例函数y=![]() 上,且DE=3,
上,且DE=3,
∴y=3,代入求得:x=2,
∴点D的坐标为(2,3).
∵C、D两点在直线y=kx+b上,
∴![]() ,
,
解得: ,
,
∴一次函数的关系式为y=![]() x+2;
x+2;
(2)由图象可知:当x<﹣6或0<x<2时,一次函数的值小于反比例函数的值.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90 ,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
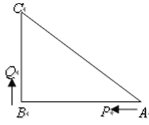
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路公交车起点站设在一居民小区附近,为了解高峰时段从该起点站乘车出行的人数,随机抽查了高峰时段10个班次从该起点站乘车的人数,结果如下:20、23、26、25、29、28、30、25、21、23.如果在高峰时段从该起点站共发车60个班次,那么估计在高峰时段从该起点站乘该路车出行的乘客一共有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE= ![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
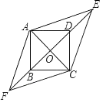
A. DE=1 B. tan∠AFO= ![]() C. AF=
C. AF= ![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
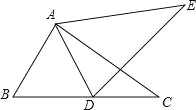
【题目】已知:如图,点B、D、C在一条直线上,AB=AD,BC=DE,AC=AE,
(1)求证:∠EAC=∠BAD.
(2)若∠BAD=42°,求∠EDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com