
【题目】在平面直角坐标系中,已知△ABC顶点坐标分别为A(0,3),B(1,1),C(﹣3,﹣1),△DEF与△ABC关于y轴对称,且A,B,C依次对应D,E,F,
(1)请写出D,E,F的坐标.
(2)在平面直角坐标系中画出△ABC和△DEF.
(3)经过计算△DEF各边长度,发现DE、EF、FD满足什么关系式,写出关系式.
(4)求△DEF的面积.
【答案】(1)D(0,3),E(-1,1),F(3,-1);(2)见解析;(3)DE2+EF2=DF2;(4)S△DEF=5.
【解析】
(1)依据△DEF与△ABC关于y轴对称,且A,B,C依次对应D,E,F,即可得到D(0,3),E(1,1),F(3,1);
(2)依据A(0,3),B(1,1),C(3,1),D(0,3),E(1,1),F(3,1),即可得到△ABC和△DEF;
(3)由勾股定理可得,DE2=5,EF2=20,DF2=25,即可得到DE、EF、FD满足:DE2+EF2=DF2;
(4)依据割补法进行计算,即可得到△DEF的面积.
(1)∵△DEF与△ABC关于y轴对称,且A,B,C依次对应D,E,F,
∴D(0,3),E(1,1),F(3,1);
(2)如图所示:△ABC和△DEF即为所求.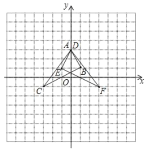
(3)由勾股定理可得,DE2=5,EF2=20,DF2=25,
∴DE、EF、FD满足:DE2+EF2=DF2;
(4)S△DEF=4×4![]() ×1×2
×1×2![]() ×2×4
×2×4![]() ×3×4=16146=5.
×3×4=16146=5.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)这个云梯的底端B离墙多远?
(2)如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路公交车起点站设在一居民小区附近,为了解高峰时段从该起点站乘车出行的人数,随机抽查了高峰时段10个班次从该起点站乘车的人数,结果如下:20、23、26、25、29、28、30、25、21、23.如果在高峰时段从该起点站共发车60个班次,那么估计在高峰时段从该起点站乘该路车出行的乘客一共有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
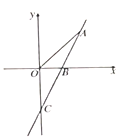
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求![]() 点的坐标和
点的坐标和![]() 的值;
的值;
(2)若点![]() 是直线
是直线![]() 第一象限部分上的一个动点,试写出
第一象限部分上的一个动点,试写出![]() 的面积与
的面积与![]() 的函数关系式;
的函数关系式;
(3)点![]() 在直线
在直线![]() 运动,当点
运动,当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积是
的面积是![]() ?求出此时
?求出此时![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
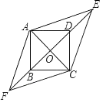
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE= ![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
A. DE=1 B. tan∠AFO= ![]() C. AF=
C. AF= ![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
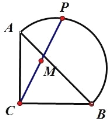
【题目】如图,在等腰 Rt△ABC 中,AC=BC=2,点 P 在以斜边 AB 为直径的半圆上,M 为 PC 的中点.当点 P 沿半圆从点A 运动至点 B 时,点 M 运动的路径长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com