
【题目】如图,抛物线y=ax2 +bx+ 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
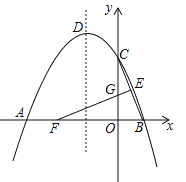
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,
△EFK的面积最大?并求出最大面积.
【答案】(1)![]() 顶点D的坐标为(-1,
顶点D的坐标为(-1,![]() )
)
(2)H(![]() ,
,![]() )
)
(3)K(-![]() ,
,![]() )
)
【解析】
(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值,进而可用配方法求出其顶点D的坐标;
(2)根据抛物线的解析式可求出C点的坐标,由于CD是定长,若△CDH的周长最小,那么CH+DH的值最小,由于EF垂直平分线段BC,那么B、C关于直线EF对称,所以BD与EF的交点即为所求的H点;易求得直线BC的解析式,关键是求出直线EF的解析式;由于E是BC的中点,根据B、C的坐标即可求出E点的坐标;可证△CEG∽△COB,根据相似三角形所得的比例线段即可求出CG、OG的长,由此可求出G点坐标,进而可用待定系数法求出直线EF的解析式,由此得解;
(3)过K作x轴的垂线,交直线EF于N;设出K点的横坐标,根据抛物线和直线EF的解析式,即可表示出K、N的纵坐标,也就能得到KN的长,以KN为底,F、E横坐标差的绝对值为高,可求出△KEF的面积,由此可得到关于△KEF的面积与K点横坐标的函数关系式,根据所得函数的性质即可求出其面积的最大值及对应的K点坐标.
(1)由题意,得![]() 解得
解得![]() ,b=-1.
,b=-1.
所以抛物线的解析式为![]() ,顶点D的坐标为(-1,
,顶点D的坐标为(-1,![]() ).
).
(2)设抛物线的对称轴与x轴交于点M.因为EF垂直平分BC,即C关于直线EG的对称点为B,连结BD交于EF于一点,则这一点为所求点H,使DH+CH最小,即最小为
DH+CH=DH+HB=BD=![]() .而
.而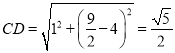 .
.
∴△CDH的周长最小值为CD+DR+CH=![]() .
.
设直线BD的解析式为y=k1x+b,则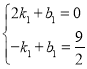 解得
解得![]() ,b1= 3.
,b1= 3.
所以直线BD的解析式为y=![]() x+ 3.
x+ 3.
由于BC= 2![]() ,CE=BC∕2 =
,CE=BC∕2 =![]() ,Rt△CEG∽△COB,
,Rt△CEG∽△COB,
得CE:CO=CG:CB,所以CG= 2.5,GO= 1.5.G(0,1.5).
同理可求得直线EF的解析式为y=![]() x+
x+![]() .
.
联立直线BD与EF的方程,解得使△CDH的周长最小的点H(![]() ,
,![]() ).
).
(3)设K(t,![]() ),xF<t<xE.过K作x轴的垂线交EF于N.
),xF<t<xE.过K作x轴的垂线交EF于N.
则KN=yK-yN=![]() -(
-(![]() t+
t+![]() )=
)=![]() .
.
所以S△EFK=S△KFN+S△KNE=![]() KN(t+ 3)+
KN(t+ 3)+![]() KN(1-t)= 2KN= -t2-3t+ 5 =-(t+
KN(1-t)= 2KN= -t2-3t+ 5 =-(t+![]() )2+
)2+![]() .
.
即当t=-![]() 时,△EFK的面积最大,最大面积为
时,△EFK的面积最大,最大面积为![]() ,此时K(-
,此时K(-![]() ,
,![]() ).
).


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
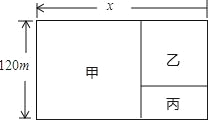
【题目】有一块长方形的土地,宽为120m,建筑商把它分成甲、乙、丙三部分,甲和乙均为正方形,现计划甲建住宅区,乙建商场,丙地开辟成面积为3200m2的公园.若设这块长方形的土地长为xm.那么根据题意列出的方程是_____.(将答案写成ax2+bx+c=0(a≠0)的形式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
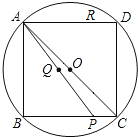
【题目】如图,![]() 内接于⊙O,
内接于⊙O,![]() ,
,![]() 是⊙O上与点
是⊙O上与点![]() 关于圆心
关于圆心![]() 成中心对称的点,
成中心对称的点,![]() 是
是![]() 边上一点,连结
边上一点,连结![]() .已知
.已知![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一动点,连结
上一动点,连结![]() 并延长交四边形
并延长交四边形![]() 的一边于点
的一边于点![]() ,且满足
,且满足![]() ,则
,则![]() 的值为_______________.
的值为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+5与x轴交于点B,与y轴交于点D,抛物线y=﹣x2+bx+c与直线y=﹣x+5交于B,D两点,点C是抛物线的顶点.

(1)求抛物线的解析式;
(2)点M是直线BD上方抛物线上的一个动点,其横坐标为m,过点M作x轴的垂线,交直线BD于点P,当线段PM的长度最大时,求m的值及PM的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为3![]() ,若存在求出点Q的坐标;若不存在请说明理由.
,若存在求出点Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为![]() .双曲线
.双曲线![]() 的图象经过BC的中点D,且与AB交于点E,连接DE.
的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com