
分析 先把分母的复合二次根式化简,再把分子部分利用因式分解的方法分解,然后约分即可.
解答 解:原式=$\frac{\sqrt{2}(\sqrt{6}-\sqrt{3}-\sqrt{2}+1)}{\sqrt{(\sqrt{2}-1)^{2}}•\sqrt{\frac{(\sqrt{3}-1)^{2}}{2}}}$
=$\frac{2[\sqrt{3}(\sqrt{2}-1)-(\sqrt{2}-1)]}{(\sqrt{2}-1)(\sqrt{3}-1)}$
=$\frac{2(\sqrt{2}-1)(\sqrt{3}-1)}{(\sqrt{2}-1)(\sqrt{3}-1)}$
=2.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
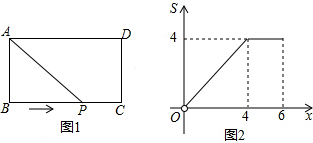
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=-1\\ y=-4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=1\\ y=-4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-1\\ y=4\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )| A. | 0 | B. | -3×($\frac{2}{3}$$\sqrt{3}$)2015 | C. | (2$\sqrt{3}$)2016 | D. | 3×($\frac{2}{3}$$\sqrt{3}$)2015 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com