
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )| A. | 0 | B. | -3×($\frac{2}{3}$$\sqrt{3}$)2015 | C. | (2$\sqrt{3}$)2016 | D. | 3×($\frac{2}{3}$$\sqrt{3}$)2015 |
分析 根据含30度的直角三角形三边的关系得OA2=$\frac{2}{\sqrt{3}}$OC2=3×$\frac{2\sqrt{3}}{3}$;OA3=$\frac{2}{\sqrt{3}}$OC3=3×($\frac{2\sqrt{3}}{3}$)2;OA4=$\frac{2}{\sqrt{3}}$OC4=3×($\frac{2\sqrt{3}}{3}$)3,于是可得到OA2016=3×($\frac{2\sqrt{3}}{3}$)2015.
解答 解:∵∠A2OC2=30°,OA1=OC2=3,
∴OA2=$\frac{2}{\sqrt{3}}$OC2=3×$\frac{2\sqrt{3}}{3}$;OA3=$\frac{2}{\sqrt{3}}$OC3=3×($\frac{2\sqrt{3}}{3}$)2;OA4=$\frac{2}{\sqrt{3}}$OC4=3×($\frac{2\sqrt{3}}{3}$)3,
∴OA2016=3×($\frac{2\sqrt{3}}{3}$)2015.
而点A2016在y轴的负半轴上,
故选B.
点评 本题考查了规律型,点的坐标:通过从一些特殊的点的坐标发现不变的因素或按规律变化的因素,然后推广到一般情况.也考查了含30度的直角三角形三边的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
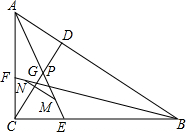 已知Rt△ABC中,CD为AB边上的高,AE、BF分别为角平分线,交CD于P、G两点,M为PE的中点,N为FG的中点,求证:MN∥AB,MN=$\frac{1}{2}$(AC+BC-AB).
已知Rt△ABC中,CD为AB边上的高,AE、BF分别为角平分线,交CD于P、G两点,M为PE的中点,N为FG的中点,求证:MN∥AB,MN=$\frac{1}{2}$(AC+BC-AB).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | M=2,N=3 | B. | M=3,N=2 | C. | M=2,N=2 | D. | M=3,N=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com