
分析 设a=2014,则原式=$\frac{1+\sqrt{a+1}(\sqrt{a}-\sqrt{a-1})}{\sqrt{a-1}+\sqrt{a}+\sqrt{a+1}}$+$\sqrt{a-1}$,再进行通分,把分子进行合并,然后把分子分解因式后约分即可.
解答 解:设a=2014,
原式=$\frac{1+\sqrt{a+1}(\sqrt{a}-\sqrt{a-1})}{\sqrt{a-1}+\sqrt{a}+\sqrt{a+1}}$+$\sqrt{a-1}$
=$\frac{1+\sqrt{a}•\sqrt{a+1}-\sqrt{a-1}•\sqrt{a+1}+a-1+\sqrt{a}•\sqrt{a-1}+\sqrt{a-1}•\sqrt{a+1}}{\sqrt{a-1}+\sqrt{a}+\sqrt{a+1}}$
=$\frac{a+\sqrt{a}•\sqrt{a-1}+\sqrt{a}•\sqrt{a+1}}{\sqrt{a-1}+\sqrt{a}+\sqrt{a+1}}$
=$\frac{\sqrt{a}(\sqrt{a-1}+\sqrt{a}+\sqrt{a+1})}{\sqrt{a-1}+\sqrt{a}+\sqrt{a+1}}$
=$\sqrt{a}$
=$\sqrt{2014}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
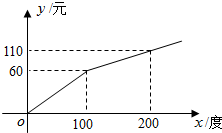 电力资源丰富,并且得到了较好的开发.某地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图象如图.
电力资源丰富,并且得到了较好的开发.某地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形网格中每个小正方形的边长都是1,每个小格的格点叫做“格点”,以格点为顶点分别按下列要求画出三角形.
如图,正方形网格中每个小正方形的边长都是1,每个小格的格点叫做“格点”,以格点为顶点分别按下列要求画出三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )| A. | 0 | B. | -3×($\frac{2}{3}$$\sqrt{3}$)2015 | C. | (2$\sqrt{3}$)2016 | D. | 3×($\frac{2}{3}$$\sqrt{3}$)2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com