
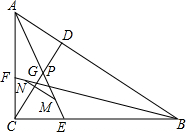
 已知Rt△ABC中,CD为AB边上的高,AE、BF分别为角平分线,交CD于P、G两点,M为PE的中点,N为FG的中点,求证:MN∥AB,MN=$\frac{1}{2}$(AC+BC-AB).
已知Rt△ABC中,CD为AB边上的高,AE、BF分别为角平分线,交CD于P、G两点,M为PE的中点,N为FG的中点,求证:MN∥AB,MN=$\frac{1}{2}$(AC+BC-AB). 分析 连接CM、CN并延长,交AB于X、Y,连接DN、DM,证明BC=BY,AC=AX和MN=$\frac{1}{2}$XY,通过推理得到答案.
解答 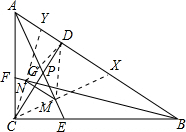 证明:连接CM、CN并延长,交AB于X、Y,连接DN、DM,
证明:连接CM、CN并延长,交AB于X、Y,连接DN、DM,
∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠BAC=90°,
∴∠BCD=∠BAC,
∵BF平分∠ABC,∴∠ABF=∠CBF,
∴∠BAC+∠ABF=∠BCD+∠CBF,
∵∠CFG=∠BAC+∠ABF,∠CGF=∠BCD+∠CBF,
∴∠CFG=∠CGF,∴CF=CG,
∵N为FG的中点,∴CN⊥FG,
∴∠BNC=∠BDC=90°,∴B、C、N、D四点共圆,
∴$\widehat{CN}$=$\widehat{DN}$,∴CN=DN,同理CM=DM,
∴MN垂直平分CD,∴MN∥AB,
∵BF平分∠ABC,BN⊥CY,
∴BC=BY,同理,AC=AX,
∴MN=$\frac{1}{2}$XY=$\frac{1}{2}$(AB-AY-BX)=$\frac{1}{2}$[AB-(AB-BY)-(AB-AX)]
=$\frac{1}{2}$(AX+BY-AB)=$\frac{1}{2}$(AC+BC-AB).
点评 本题考查的是三角形中位线定理和四点共圆的知识,掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=-1\\ y=-4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=1\\ y=-4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-1\\ y=4\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
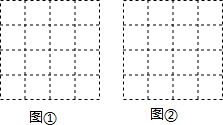 如图,正方形网格中每个小正方形的边长都是1,每个小格的格点叫做“格点”,以格点为顶点分别按下列要求画出三角形.
如图,正方形网格中每个小正方形的边长都是1,每个小格的格点叫做“格点”,以格点为顶点分别按下列要求画出三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )| A. | 0 | B. | -3×($\frac{2}{3}$$\sqrt{3}$)2015 | C. | (2$\sqrt{3}$)2016 | D. | 3×($\frac{2}{3}$$\sqrt{3}$)2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
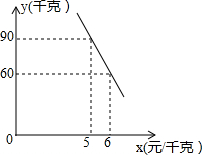 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.| 蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
| 所付的金额(元) | … | 125 | 300 | 300 | 360 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com