
分析 已知等腰三角形的一腰上的中线把这个三角形的周长分为12和15两部分,由于没有具体说明哪部分是12,哪部分是15;所以需分两种情况进行分析:第一种AB+AD=12,第二种AB+AD=15;由此可分别求得三角形的三边的长.
解答 解:在△ABC中,AB=AC,BD是中线,设AB=x,BC=y
(1)当AB+AD=12时,则$\left\{\begin{array}{l}{x+\frac{1}{2}x=12}\\{y+\frac{1}{2}x=15}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=8}\\{y=11}\end{array}\right.$,
∴三角形三边的长为8、8、11;
(2)当AB+AD=15时,则$\left\{\begin{array}{l}{x+\frac{1}{2}x=15}\\{y+\frac{1}{2}x=12}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=10}\\{y=7}\end{array}\right.$,
∴三角形三边的长为10、10、7
经检验,两种情况均符合三角形三边关系定理
因此这个三角形的腰长,底边长分别为8,11或10,7.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )| A. | 0 | B. | -3×($\frac{2}{3}$$\sqrt{3}$)2015 | C. | (2$\sqrt{3}$)2016 | D. | 3×($\frac{2}{3}$$\sqrt{3}$)2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
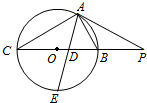 如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2.14既是负数、分数,也是有理数 | |
| B. | 0既不是正数也不是负数,但是整数 | |
| C. | 0是非正数 | |
| D. | -2012既是负数,也是整数,但不是有理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com