练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，∠BOD＝45°，那么不大于90°的角有___个，它们的度数之和是____．

    【答案】10 450°

    【解析】

    (1)∠AOE＝90°，故图中所有的角都是不大于90°的角；

    (2)将所有的角相加，发现有的角相加等于∠EOA，即和为90°，而有的角相加等于∠BOD，即和为45°，将这样的角凑在一起计算，即可求出所有角的度数.

    不大于 90°的角有∠EOD，∠EOC，∠EOB，∠EOA，∠DOC，∠DOB，∠DOA，∠COB，∠COA，∠BOA共10个；

    它们的度数之和是(∠EOD＋∠DOA)＋(∠EOC＋∠COA)＋(∠ EOB＋∠BOA)＋[(∠DOC＋∠COB)＋∠DOB]＋∠EOA＝90°＋90°＋90°＋(45°＋45°)＋90°＝450°.

    故答案为10；450°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

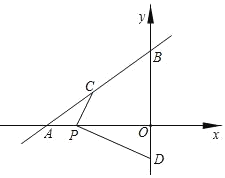
    【题目】如图，直线与x轴、y轴分别交于点A和点B，点C在线段AB上，点D在y轴的负半轴上，C、D两点到x轴的距离均为2．

    （1）点C的坐标为　 　　，点D的坐标为　 　 　；

    （2）点P为线段OA上的一动点，当PC+PD最小时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的材料

    勾股定理神秘而美妙，它的证法多种多样，下面是教材中介绍的一种拼图证明勾股定理的方法.

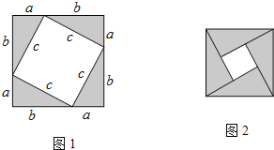
    先做四个全等的直角三角形，设它们的两条直角边分别为a,b，斜边为c，然后按图1的方法将它们摆成正方形.

    由图1可以得到，

    整理，得．

    所以．

    （1）如果把图1中的四个全等的直角三角形摆成图2所示的正方形，

    请你参照上述证明勾股定理的方法，用图2证明勾股定理.

    （2）图2中若大正方形的面积是13,小正方形的面积是1,求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：关于x的方程：mx2﹣（3m﹣1）x+2m﹣2=0．

    （1）求证：无论m取何值时，方程恒有实数根；

    （2）若关于x的二次函数y=mx2﹣（3m﹣1）x+2m﹣2的图象与x轴两交点间的距离为2时，求抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开始调出物资（调进物资与调出物资的速度均保持不变）.储运部库存物资（吨）与时间（小时）之间的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是（ ）

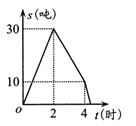
    A. 4小时B. 4.3小时C. 4.4小时D. 5小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在数轴上有A、B、C三个点，请回答:

    （1）将A点向右移动3个单位长度，C点向左移动5个单位长度，它们各自表示新的什么数？

    （2）移动A、B、C中的两个点，使得三个点表示的数相同，有几种移动方法？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算

    (1)6－（＋3）－（－7）＋（－2）;

    (2)(－－＋)×(－36)

    (3) (﹣2)2+3×（﹣1）2016﹣（﹣4）×2 .

    (4)6x2y－(－2x2y)

    (5)(3a－2) －2(a－1)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆汽车和一辆摩托车分别从A，B两地去同一个城市，它们离A地的路程随时间变化的图象如图所示．则下列结论：①摩托车比汽车晚到1h；②A，B两地的路程为20km；③摩托车的速度为45km/h，汽车的速度为60km/h；④汽车出发1小时后与摩托车相遇，此时距B地40千米．其中正确结论的个数是(　　)

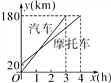
    A. 2个 B. 3个 C. 4个 D. 1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在正方形ABCD中，E是AB上一点，G是AD上一点，∠ECG=45°，求证EG=BE+GD．

    （2）请用（1）的经验和知识完成此题：如图2，在四边形ABCD中，AG//BC(BC>AG)，∠B=90°，AB=BC=12，E是AB上一点，且∠ECG=45°，BE=4，求EG的长？

    查看答案和解析>>

    同步练习册答案