
【题目】(探索发现)有绝对值的定义可得,数轴上表示数![]() 的点到原点的距离为
的点到原点的距离为![]() .小丽进一步探究发现,在数轴上,表示3和5的两点之间的距离为
.小丽进一步探究发现,在数轴上,表示3和5的两点之间的距离为![]() ;表示
;表示![]() 和5的两点之间的距离为
和5的两点之间的距离为![]() ;表示
;表示![]() 和
和![]() 的两点之间的距离为
的两点之间的距离为![]() .
.
(概括总结)根据以上过程可以得出:数轴上,表示数![]() 和数
和数![]() 的两点之间的距离为
的两点之间的距离为![]() .
.
(问题解决)
(1)若![]() ,则
,则![]() ________;
________;
(2)若![]() ,则
,则![]() ________;
________;
(3)若![]() ,则
,则![]() ________.
________.
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳麓山是旅游胜地,据统计2019年9月30日岳麓山旅游人数为2万人,十一黄金周期间,岳麓山7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):

(1)请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?
(2)求这7天去岳麓山旅游的总人数
查看答案和解析>>
科目:初中数学 来源: 题型:
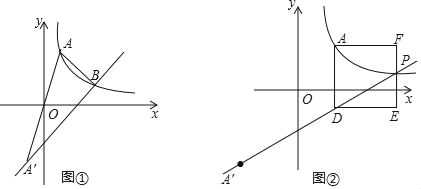
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
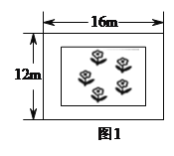
【题目】在一块长![]() ,宽为
,宽为![]() 的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
(![]() )小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
)小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
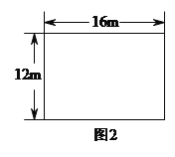
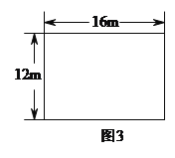
(![]() )小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图
)小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图![]() 和图
和图![]() 中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣2.5表示的点与数 表示的点重合;
(2)若﹣1表示的点与5表示的点重合,回答以下问题:
①5表示的点与数 表示的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为![]() ,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为
,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为![]() 时,正方形EFGH的面积的所有可能值是_____(不包括5).
时,正方形EFGH的面积的所有可能值是_____(不包括5).
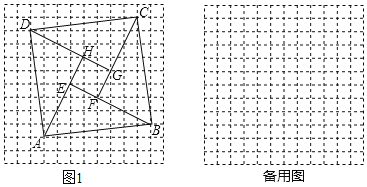
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程mx2-2mx+m-2=0.
(1)若方程有两个不等实数根,求m的取值范围;
(2)若方程的两实数根为x1,x2,且|x1-x2|=1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+6(a≠0)与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.
(1)求抛物线y的函数表达式及点C的坐标;
(2)点M为坐标平面内一点,若MA=MB=MC,求点M的坐标;
(3)在抛物线上是否存在点E,使![]() ∠ABE=
∠ABE=![]() ∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
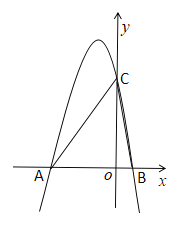
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com