
【题目】如图,已知抛物线y=ax2+bx+6(a≠0)与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.
(1)求抛物线y的函数表达式及点C的坐标;
(2)点M为坐标平面内一点,若MA=MB=MC,求点M的坐标;
(3)在抛物线上是否存在点E,使![]() ∠ABE=
∠ABE=![]() ∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
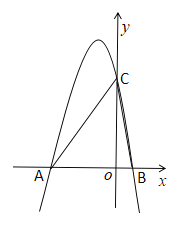
【答案】(1)y=-2x2-4x+6;(2)M(-1,![]() );(3)E1(-2,6),E2(-4,-10) .
);(3)E1(-2,6),E2(-4,-10) .
【解析】(1)根据抛物线过A、B两点,待定系数法求解可得;;
(2)由(1)知抛物线对称轴为直线x=-1,设H为AC的中点,求出直线AC的垂直平分线的解析式即可得解;
(3)①过点A作![]() 交y轴于点F,交CB的延长线于点D,证明ΔAOF∽ΔCOA,求得
交y轴于点F,交CB的延长线于点D,证明ΔAOF∽ΔCOA,求得![]() ,分别求出直线AF、BC的解析式的交点
,分别求出直线AF、BC的解析式的交点![]() ,求出
,求出![]() ,
,
根据![]() ∠ABE=
∠ABE=![]() ∠ACB求出
∠ACB求出![]() ∠ABE=2,易求E点坐标.
∠ABE=2,易求E点坐标.
(1)把A(-3,0)、B(1,0)代入y=ax2+bx+6得,
![]() ,解得
,解得![]()
∴y=-2x2-4x+6,
令x=0,则y=6,
∴C(0,6);
(2)![]() =-2(x+1)2+8,
=-2(x+1)2+8,
∴抛物线的对称轴为直线x=-1.
设H为线段AC的中点,故H(![]() ,3).
,3).
设直线AC的解析式为:y=kx+m,则有
![]() ,解得,
,解得,![]() ,
,
∴y=2x+6
设过H点与AC垂直的直线解析式为:![]() ,
,
∴![]()
∴b=![]()
∴![]()
∴当x=-1时,y=![]()
∴M(-1,![]() )
)
(3)①过点A作![]() 交y轴于点F,交CB的延长线于点D
交y轴于点F,交CB的延长线于点D
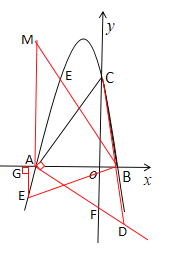
∵∠ACO+∠CAO=90°,∠DAO+∠CAO=90°
∴∠DAO=∠ACO
∵∠ACO=∠ACO
∴ΔAOF∽ΔCOA
∴![]()
∴![]()
∵OA=3,OC=6
∴![]()
∴![]()
直线AF的解析式为:![]()
直线BC的解析式为:![]()
∴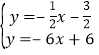 ,解得
,解得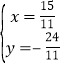
∴![]()
∴![]()
∴![]() ∠ACB=
∠ACB=![]()
∵![]() ∠ABE=
∠ABE=![]() ∠ACB
∠ACB
∴![]() ∠ABE=2
∠ABE=2
过点A作![]() 轴,连接BM交抛物线于点E
轴,连接BM交抛物线于点E
∵AB=4,![]() ∠ABE=2
∠ABE=2
∴AM=8
∴M(-3,8)
直线BM的解析式为:![]()
∴![]() ,解得
,解得![]()
∴y=6
∴E(-2,6)
②当点E在x轴下方时,过点E作![]() ,连接BE,设点E
,连接BE,设点E![]()
∴![]() ∠ABE=
∠ABE=![]() 2
2
∴m=-4或m=1(舍去)
可得E(-4,-10)
综上所述E1(-2,6),E2(-4,-10)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(探索发现)有绝对值的定义可得,数轴上表示数![]() 的点到原点的距离为
的点到原点的距离为![]() .小丽进一步探究发现,在数轴上,表示3和5的两点之间的距离为
.小丽进一步探究发现,在数轴上,表示3和5的两点之间的距离为![]() ;表示
;表示![]() 和5的两点之间的距离为
和5的两点之间的距离为![]() ;表示
;表示![]() 和
和![]() 的两点之间的距离为
的两点之间的距离为![]() .
.
(概括总结)根据以上过程可以得出:数轴上,表示数![]() 和数
和数![]() 的两点之间的距离为
的两点之间的距离为![]() .
.
(问题解决)
(1)若![]() ,则
,则![]() ________;
________;
(2)若![]() ,则
,则![]() ________;
________;
(3)若![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】来自某综合市场财务部的报告表明,商场2014年1﹣4月份的投资总额一共是2065万元,商场2014年第一季度每月利润统计图和2014年1﹣4月份利润率统计图如下(利润率=利润÷投资金额).则商场2014年4月份利润是__万元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线EF分别与直线AB,CD相交于点E,F,AB∥CD,EM平分∠BEF,FM平分∠EFD.
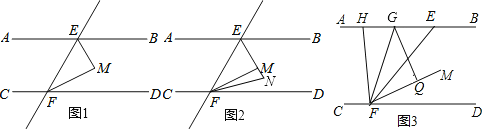
(1)求证:∠EMF=90°.
(2)如图2,若FN平分∠MFD交EM的延长线于点N,且∠BEN与∠EFN的比为4:3,求∠N的度数.
(3)如图3,若点H是射线EA之间一动点,FG平分∠HFE,过点G作GQ⊥EM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
①8+(﹣10)+(﹣2)﹣(﹣5)
②2![]() ﹣3
﹣3![]() ﹣5
﹣5![]() ﹣|﹣3
﹣|﹣3![]() |
|
③(﹣1![]() )+1.25+(﹣8.5)+10
)+1.25+(﹣8.5)+10![]()
④(![]() )×(﹣12)
)×(﹣12)
⑤(﹣199![]() )×5(用简便方法计算)
)×5(用简便方法计算)
⑥10×(﹣![]() )﹣2×
)﹣2×![]() +(﹣3)×(﹣
+(﹣3)×(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
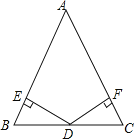
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,先填空后证明.
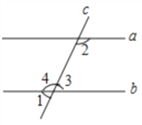
已知: ∠1+∠2=180° 求证:a∥b.
证明:∵ ∠1=∠3(_____),∠1+∠2=180°(_____),
∴ ∠3+∠2=180°(______).
∴ a∥b(_____).
请你再写出一种证明方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC 的顶点 A (-2,0),点 B,C分别在x轴和y轴的正半轴上,∠ACB=90°,∠BAC=60°
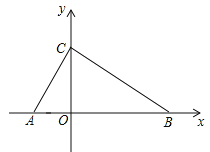
(1)求点 B 的坐标;
(2)点 P 为 AC延长线上一点,过 P 作PQ∥x轴交 BC 的延长线于点 Q ,若点 P 的横坐标为t,线段PQ的长为d,请用含t的式子表示d;
(3) 在(2)的条件下,当PA=![]() d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com