
【题目】如图1,已知直线EF分别与直线AB,CD相交于点E,F,AB∥CD,EM平分∠BEF,FM平分∠EFD.
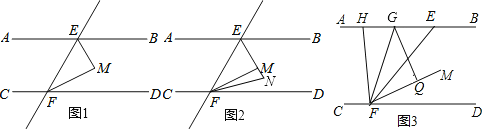
(1)求证:∠EMF=90°.
(2)如图2,若FN平分∠MFD交EM的延长线于点N,且∠BEN与∠EFN的比为4:3,求∠N的度数.
(3)如图3,若点H是射线EA之间一动点,FG平分∠HFE,过点G作GQ⊥EM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.
【答案】(1)见解析;(2)∠N=75°;(3)无论点H在何处都有∠EHF=2∠FGQ.证明见解析.
【解析】
(1)根据两直线平行,同旁内角互补,以及角平分线定义进行判断即可;
(2)如图2中,由题意可以假设:∠BEN=4x,∠EFN=3x,根据∠MFE=∠MFD列出方程,求出x即可得到∠N的度数;
(3)先根据题意得到∠GFQ=90°﹣∠FGQ,再根据FG平分∠HFE,FM平分∠EFD,即可得出∠HFD=2∠GFQ,最后根据∠EHF+∠HFD=180°,即可得出∠EHF=2∠FGQ.
(1)如图1中,∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵EM平分∠BEF,FM平分∠EFD,
∴∠FEM=![]() ∠BEF,∠EFM=
∠BEF,∠EFM=![]() ∠DFE,
∠DFE,
∴∠FEM+∠EFM=![]() ×180°=90°,
×180°=90°,
∴∠EMF=90°;
(2)如图2中,由题意可以假设:∠BEN=4x,∠EFN=3x,
∵∠EMF=90°,∠FEM=∠MEB=4x,
∴∠EFM=90°﹣4x,
∴∠NFM=∠NFD=3x﹣(90°﹣4x)=7x﹣90°,
∵∠MFE=2∠MFD,
∴90°﹣4x=2(7x﹣90°),
∴x=15°,
∴∠MFN=15°,
∴∠N=90°﹣15°=75°;
(3)如图3,∵GQ⊥FM,
∴∠GFQ+∠FGQ=180°﹣90°=90°(三角形的内角和等于180°).
∴∠GFQ=90°﹣∠FGQ.
∵FG平分∠HFE,FM平分∠EFD,
又∵∠GFQ=∠GFE+∠QFE=![]() (∠HFE+∠EFD)=
(∠HFE+∠EFD)=![]() ∠HFD,
∠HFD,
∴∠HFD=2∠GFQ.
又∵AB∥CD,
∴∠EHF+∠HFD=180°,
∴∠EHF=180°﹣∠HFD=180°﹣2∠GFQ=180°﹣2(90°﹣∠FGQ)=2∠FGQ,
即无论点H在何处都有∠EHF=2∠FGQ.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在一块长![]() ,宽为
,宽为![]() 的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
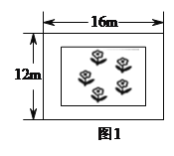
(![]() )小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
)小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
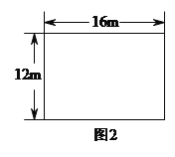
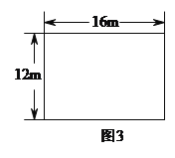
(![]() )小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图
)小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图![]() 和图
和图![]() 中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
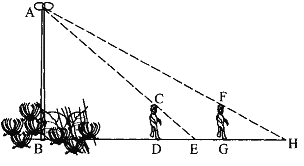
查看答案和解析>>
科目:初中数学 来源: 题型:
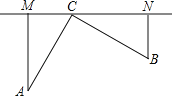
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥NN于点M,BN⊥MN于N.
(1)求证:△AMC≌△CNB;
(2)求证:MN=AM+BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有1500名学生,小明想了解全校学生每月课外阅读书籍的数量情况,随机抽取了部分学生,得到如统计图:
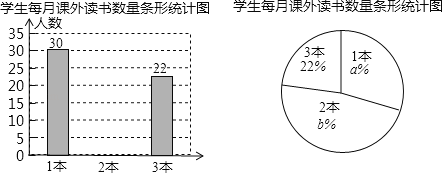
(1)一共抽查了多少人?
(2)每月课外阅读书籍数量是1本的学生对应的圆心角度数是多少?
(3)估计该校全体学生每月课外阅读书籍的总量大约是多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+6(a≠0)与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.
(1)求抛物线y的函数表达式及点C的坐标;
(2)点M为坐标平面内一点,若MA=MB=MC,求点M的坐标;
(3)在抛物线上是否存在点E,使![]() ∠ABE=
∠ABE=![]() ∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
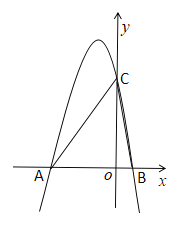
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
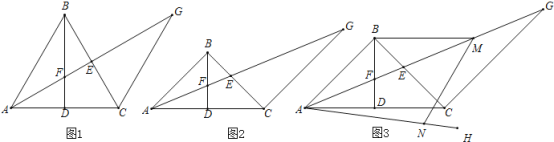
(1)如图1,若∠ABC=60°,求证:AF=![]() EG;
EG;
(2)如图2,若∠ABC=90°,求证:AF=![]() EG;
EG;
(3)在(2)的条件下如图3,过点A作∠CAH=![]() ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com