
【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
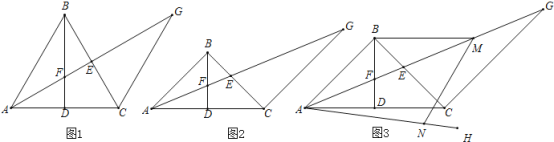
(1)如图1,若∠ABC=60°,求证:AF=![]() EG;
EG;
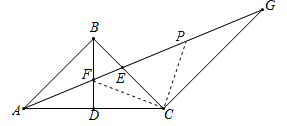
(2)如图2,若∠ABC=90°,求证:AF=![]() EG;
EG;
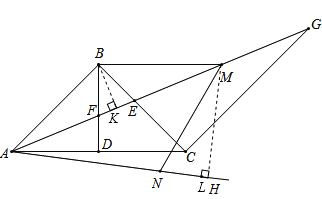
(3)在(2)的条件下如图3,过点A作∠CAH=![]() ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,![]() ,求BN的长.
,求BN的长.
【答案】(1)证明见解析;(2)证明见解析;(3)6.
【解析】
(1)先判断出△ABC是等边三角形,设DF=a,表示出AF、EF,根据两直线平行,内错角相等求出∠G=∠CAE=30°,表示出GE,然后相比即可;
(2)取EG的中点P,连接CF、CP,根据角平分线的定义求出∠BAE=∠FAC=22.5°,根据等腰直角三角形的对称性可得AF=CF,然后求出∠CFP=45°,再求出∠ECG=90°,根据直角三角形斜边上的中线等于斜边的一半可得CP=GP=![]() EG,根据两直线平行,内错角相等可得∠G=∠BAE=22.5°,再求出∠CPF=45°,根据等角对等边可得CF=CP,从而得到AF=CP,AF=
EG,根据两直线平行,内错角相等可得∠G=∠BAE=22.5°,再求出∠CPF=45°,根据等角对等边可得CF=CP,从而得到AF=CP,AF=![]() EG,整理即可得证;
EG,整理即可得证;
(3)过点B作BK⊥AM于K,过点M作ML⊥AH于H,先求出∠EAH=30°,根据直角三角形两锐角互余求出∠AML=∠BMN=60°,然后求出∠BMK=∠NML,再求出∠BAE=∠BME=22.5°,根据等角对等边可得AB=BM,根据等腰三角形三线合一的性质可得MK=![]() AM,根据直角三角形斜边上的中线等于斜边的一半可得ML=
AM,根据直角三角形斜边上的中线等于斜边的一半可得ML=![]() AM,从而得到MK=ML,再利用“角边角”证明△BMK和△NML全等,根据全等三角形对应边相等可得MN=BM,再根据等腰直角三角形的面积求出AB,再判断出△BMN是等边三角形,然后求解即可.
AM,从而得到MK=ML,再利用“角边角”证明△BMK和△NML全等,根据全等三角形对应边相等可得MN=BM,再根据等腰直角三角形的面积求出AB,再判断出△BMN是等边三角形,然后求解即可.
(1)证明:∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
设DF=a,
∵BD为△ABC的中线,AE为△ABC的角平分线,
∴AF=2a,EF=a,
∵CG∥AB,
∴∠G=∠CAE=∠CAE=30°,
∴GE=AE=AF+EF=2a+a=3a,
∴AF=![]() EG;
EG;
(2)证明:取EG的中点P,连接CF、CP,
∵BA=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴AF=CF,
∵AF是△ABC的角平分线,
∴∠BAE=∠FAC=22.5°,
∴∠CFP=45°,
∵CG∥AB,
∴∠ECG=∠ABC=90°,
∴CP=GP=![]() EG,
EG,
∵CG∥AB,
∴∠G=∠BAE=22.5°,
∴∠CPF=45°,
∴CF=CP,
∴AF=![]() EG;
EG;
(3)过点B作BK⊥AM于K,过点M作ML⊥AH于H,
∵∠CAH=![]() ∠FAC,
∠FAC,
∴∠EAH=22.5°+![]() ×22.5°=30°,
×22.5°=30°,
∴∠AML=90°-30°=60°,
∵∠BMN与∠EAH互余,
∴∠BMN=90°-30°=60°,
∴∠BMK=∠NML,
∵AE是△ABC的平分线,CG∥AB,
∴∠BAE=∠BME=![]() ×45°=22.5°,
×45°=22.5°,
∴AB=BM,
∴MK=![]() AM,
AM,
∵∠MAH=30°,ML⊥AH,
∴MH=![]() AM,
AM,
∴MK=ML,
在△BMK和△NML中,
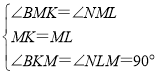 ,
,
∴△BMK≌△NML(ASA),
∴MN=BM,
∴MN=AB,
∵△ABC的面积为18,
∴![]() AB2=18,
AB2=18,
∴AB=6,
∵∠BMN=60°,BM=MN,
∴△BMN是等边三角形,
∴BN=MN=6.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知直线EF分别与直线AB,CD相交于点E,F,AB∥CD,EM平分∠BEF,FM平分∠EFD.
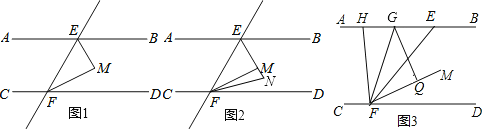
(1)求证:∠EMF=90°.
(2)如图2,若FN平分∠MFD交EM的延长线于点N,且∠BEN与∠EFN的比为4:3,求∠N的度数.
(3)如图3,若点H是射线EA之间一动点,FG平分∠HFE,过点G作GQ⊥EM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
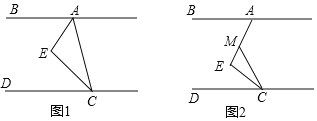
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=AB,∠BAC=90°,D是AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,则EC=______
,则EC=______
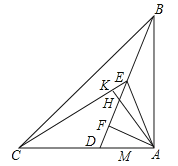
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC 的顶点 A (-2,0),点 B,C分别在x轴和y轴的正半轴上,∠ACB=90°,∠BAC=60°
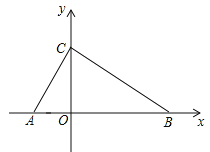
(1)求点 B 的坐标;
(2)点 P 为 AC延长线上一点,过 P 作PQ∥x轴交 BC 的延长线于点 Q ,若点 P 的横坐标为t,线段PQ的长为d,请用含t的式子表示d;
(3) 在(2)的条件下,当PA=![]() d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
d时,E是线段CQ上一点,连接OE,BP,若OE=BP,求∠APB-∠OEB的度数..
查看答案和解析>>
科目:初中数学 来源: 题型:
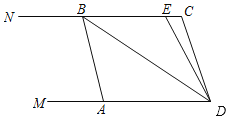
【题目】如图,已知两条直线DM∥CN,线段AB的两个端点A、B分别在直线OM、CN上,∠C=∠BAD,点E在线段BC上,且DB平分∠ADE.
(1)求证:AB∥CD;
(2)若沿着NC方向平移线段AB,那么∠CBD与∠CED度数之间的关系是否随着AB位置的变化而变化?若变化,请找出变化规律;若不变化,请确定它们之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
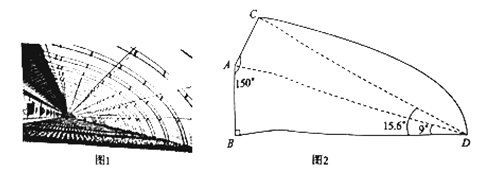
【题目】随着我市农产品整体品牌形象“聊·胜一筹!”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图1.线段![]() ,
,![]() 分别表示大棚的墙高和跨度,
分别表示大棚的墙高和跨度,![]() 表示保温板的长.已知墙高
表示保温板的长.已知墙高![]() 为2米,墙面与保温板所成的角
为2米,墙面与保温板所成的角![]() ,在点
,在点![]() 处测得
处测得![]() 点、
点、![]() 点的仰角分别为
点的仰角分别为![]() ,
,![]() ,如图2.求保温板
,如图2.求保温板![]() 的长是多少米?(精确到0.1米)
的长是多少米?(精确到0.1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com