
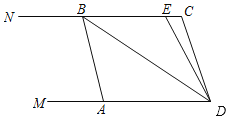
【题目】如图,已知两条直线DM∥CN,线段AB的两个端点A、B分别在直线OM、CN上,∠C=∠BAD,点E在线段BC上,且DB平分∠ADE.
(1)求证:AB∥CD;
(2)若沿着NC方向平移线段AB,那么∠CBD与∠CED度数之间的关系是否随着AB位置的变化而变化?若变化,请找出变化规律;若不变化,请确定它们之间的数量关系.
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足![]() ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
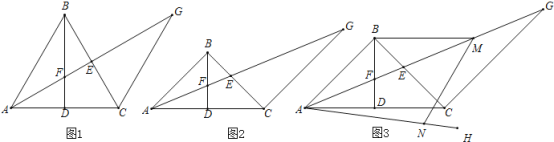
(1)如图1,若∠ABC=60°,求证:AF=![]() EG;
EG;
(2)如图2,若∠ABC=90°,求证:AF=![]() EG;
EG;
(3)在(2)的条件下如图3,过点A作∠CAH=![]() ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过![]() 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍![]() ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
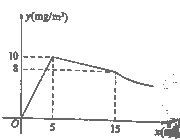
A. 经过![]() 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到![]()
B. 室内空气中的含药量不低于![]() 的持续时间达到了
的持续时间达到了![]()
C. 当室内空气中的含药量不低于![]() 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D. 当室内空气中的含药量低于![]() 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到![]() 开始,需经过
开始,需经过![]() 后,学生才能进入室内
后,学生才能进入室内
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com