
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
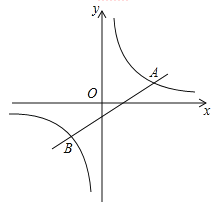
(1)求一次函数与反比例函数的解析式;
(2) 请根据图象直接写出![]() 时
时![]() 的取值范围.
的取值范围.
【答案】反比例函数的解析式为y2=![]() .一次函数的解析式为y=
.一次函数的解析式为y=![]() x﹣1.(2)x<﹣2或0<x<4.
x﹣1.(2)x<﹣2或0<x<4.
【解析】(1)由点A的坐标利用反比例函数图象上点的坐标特征可求出k2的值,进而可得出反比例函数的解析式,由点B的纵坐标结合反比例函数图象上点的坐标特征可求出点B的坐标,再由点A、B的坐标利用待定系数法,即可求出一次函数的解析式;
(2)根据两函数图象的上下位置关系,找出y1<y2时x的取值范围.
(1)∵反比例函数y2=![]() (k2≠0)的图象过点A(4,1),
(k2≠0)的图象过点A(4,1),
∴k2=4×1=4,
∴反比例函数的解析式为y2=![]() ,
,
∵点B(n,﹣2)在反比例函数y2=![]() 的图象上,
的图象上,
∴n=4÷(﹣2)=﹣2,
∴点B的坐标为(﹣2,﹣2),
将A(4,1)、B(﹣2,﹣2)代入y1=k1x+b,
![]() ,解得:
,解得: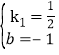 ,
,
∴一次函数的解析式为y=![]() x﹣1;
x﹣1;
(2)观察函数图象,可知:当x<﹣2和0<x<4时,一次函数图象在反比例函数图象下方,
∴y1<y2时x的取值范围为x<﹣2或0<x<4.


科目:初中数学 来源: 题型:
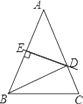
【题目】如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
(1)若∠A=46°,求∠CBD的度数;
(2)若AB=8,△CBD周长为13,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线EF分别与直线AB,CD相交于点E,F,AB∥CD,EM平分∠BEF,FM平分∠EFD.
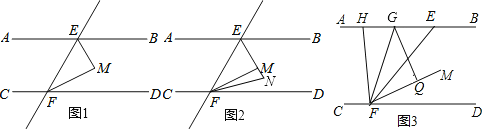
(1)求证:∠EMF=90°.
(2)如图2,若FN平分∠MFD交EM的延长线于点N,且∠BEN与∠EFN的比为4:3,求∠N的度数.
(3)如图3,若点H是射线EA之间一动点,FG平分∠HFE,过点G作GQ⊥EM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
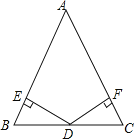
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,先填空后证明.
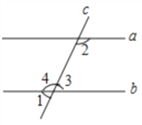
已知: ∠1+∠2=180° 求证:a∥b.
证明:∵ ∠1=∠3(_____),∠1+∠2=180°(_____),
∴ ∠3+∠2=180°(______).
∴ a∥b(_____).
请你再写出一种证明方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
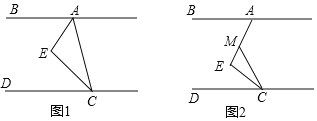
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
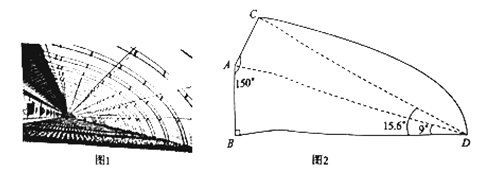
【题目】随着我市农产品整体品牌形象“聊·胜一筹!”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图1.线段![]() ,
,![]() 分别表示大棚的墙高和跨度,
分别表示大棚的墙高和跨度,![]() 表示保温板的长.已知墙高
表示保温板的长.已知墙高![]() 为2米,墙面与保温板所成的角
为2米,墙面与保温板所成的角![]() ,在点
,在点![]() 处测得
处测得![]() 点、
点、![]() 点的仰角分别为
点的仰角分别为![]() ,
,![]() ,如图2.求保温板
,如图2.求保温板![]() 的长是多少米?(精确到0.1米)
的长是多少米?(精确到0.1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com