练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

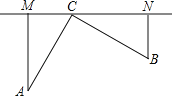
    【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC，过点C在△ABC外作直线MN，AM⊥NN于点M，BN⊥MN于N．

    （1）求证：△AMC≌△CNB；

    （2）求证：MN＝AM+BN．

    【答案】（1）见解析；（2）见解析

    【解析】

    （1）首先根据题干条件求出∠2＝∠1，∠4＝∠5，结合AC=BC，即可证明△BNC≌△CMA；（2）由（1）得到AM＝CN，CM＝BN，即可证明出结论．

    证明：（1）如图：

    ∵AM⊥MN，BN⊥MN，

    ∴∠4＝∠5＝90°，∠2+∠3＝90，

    ∵∠ACB＝90°，

    ∴∠1+∠3＝90，

    ∴∠2＝∠1，

    在△AMC和△CNB中

    ，

    ∴△AMC≌△CNB（AAS）；

    （2）由（1）得△AMC≌△CNB，

    ∴AM＝CN，CM＝BN，

    ∴MN＝CN+CM＝AM+BN

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，点A(m,2)在直线:y=2x上，过点A的直线与x轴交于点B(4,0).

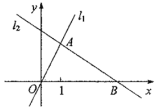
    (1)求直线的解析式;

    (2)己知点P.的坐标为（n,0）,过点P垂直x轴的直线与,分别交于点C,D，当点C位于点D上方时，求n的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

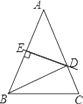
    【题目】如图，△ABC中，AB=AC，AB的垂直平分线DE分别交AC、AB于点D、E．

    （1）若∠A=46°，求∠CBD的度数；

    （2）若AB=8，△CBD周长为13，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图已知：E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．求证：

    （1）∠ECD=∠EDC；

    （2）OE是CD的垂直平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

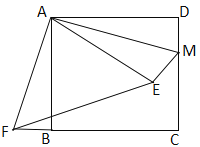
    【题目】如图，在正方形ABCD中，AB=3，点M在CD的边上，且DM=1，ΔAEM与ΔADM关于AM所在的直线对称，将ΔADM按顺时针方向绕点A旋转90°得到ΔABF，连接EF，则线段EF的长为（ ）

    A. 3 B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】来自某综合市场财务部的报告表明，商场2014年1﹣4月份的投资总额一共是2065万元，商场2014年第一季度每月利润统计图和2014年1﹣4月份利润率统计图如下（利润率＝利润÷投资金额）．则商场2014年4月份利润是__万元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知直线EF分别与直线AB，CD相交于点E，F，AB∥CD，EM平分∠BEF，FM平分∠EFD.

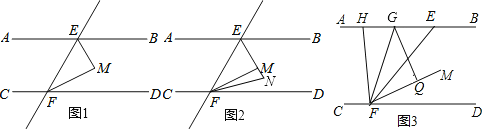
    （1）求证：∠EMF＝90°．

    （2）如图2，若FN平分∠MFD交EM的延长线于点N，且∠BEN与∠EFN的比为4：3，求∠N的度数．

    （3）如图3，若点H是射线EA之间一动点，FG平分∠HFE，过点G作GQ⊥EM于点Q，请猜想∠EHF与∠FGQ的关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．

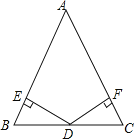
    （1）求证：DE=DF；

    （2）若∠A=60°，BE=1，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB=90°，AC=AN，BC=BM，则∠MCN=( )

    A. 30°B. 45°C. 60°D. 55°

    查看答案和解析>>

    同步练习册答案