
【题目】如图,AB是⊙O的直径,C为⊙O上一点,CD平分∠ACB交⊙O于点D.
(1)AD与BD相等吗?为什么?
(2)若AB=10,AC=6,求CD的长;
(3)若P为⊙O上异于A、B、C、D的点,试探究PA、PD、PB之间的数量关系.

【答案】(1)AD=BD,理由见解析;
(2)CD=![]() ;
;
(3)①当点P在![]() 上时, PA+PB=
上时, PA+PB=![]() PD;②当点P在
PD;②当点P在![]() 上时, PA﹣PB=
上时, PA﹣PB=![]() PD.③当点P在
PD.③当点P在![]() 上时, PB﹣PA=
上时, PB﹣PA=![]() PD.
PD.
【解析】试题分析:(1)结论:AD=BD.只要证明![]() 即可.
即可.
(2)如图2中,作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.由Rt△AFD≌Rt△BGD(HL),推出AF=BG,由Rt△CDF≌Rt△CDG(HL),推出CF=CG,由△CDF是等腰直角三角形,得CD=![]() CF,求出CF即可解决问题.
CF,求出CF即可解决问题.
(3)分三种情形讨论①如图3中,当点P在![]() 上时,结论:PA+PB=
上时,结论:PA+PB=![]() PD;②如图4中,当点P在
PD;②如图4中,当点P在![]() 上时,结论:PA-PB=
上时,结论:PA-PB=![]() PD;③如图5中,当点P在
PD;③如图5中,当点P在![]() 上时,结论:PB-PA=
上时,结论:PB-PA=![]() PD.
PD.
试题解析:(1)结论:AD=BD.
理由:如图1中,
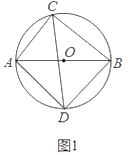
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,
![]() ,
,
∴DA=DB.
(2)如图2中,作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
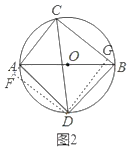
∵∠AFD=∠BGD=90°,
在Rt![]() ,
,
∴Rt△AFD≌Rt△BGD(HL),
∴AF=BG.
同理:Rt△CDF≌Rt△CDG(HL),
∴CF=CG.
∵AB是直径,
∴∠ACB=90°,
∵AC=6,AB=10,
∴BC=![]() =8,
=8,
∴6+AF=8﹣AF,
∴AF=1,
∴CF=7,
∵CD平分∠ACB,
∴∠ACD=45°,
∵△CDF是等腰直角三角形,
∴CD=![]() ,CF=7
,CF=7![]() .
.
(3)①如图3中,当点P在![]() 上时,结论:PA+PB=
上时,结论:PA+PB=![]() PD.
PD.
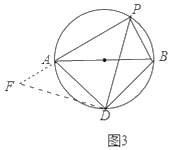
理由:将△PDB绕点D逆时针旋转90°得到△FAD,
∵∠PAB+∠PBD=180°,∠FAD=∠PBD,
∴∠FAD+∠PAD=180°,
∴P、A、F共线,
∵∠F=∠DPB=∠BAD=45°,
∴△PDF是等腰直角三角形,
∴PF=![]() PD,
PD,
∵PB=AF,
∴PF=PA+AF=PA+PB=![]() PD.,
PD.,
∴PA+PB=![]() PD.
PD.
②如图4中,当点P在![]() 上时,结论:PA﹣PB=
上时,结论:PA﹣PB=![]() PD.
PD.
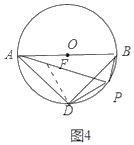
理由:在AP上取一点F,使得AF=PB,
在△FAD和△PBD中,  ,
,
∴△FAD≌△PBD,
∴DF=DP,∠ADF=∠BDP,
∠FDP=∠ADB=90°,
∴△FDP是等腰直角三角形,
∴PF=![]() PD,
PD,
∴PA﹣PB=PA﹣AF=PF=![]() PD,
PD,
∴PA﹣PB=![]() PD.
PD.
③如图5中,当点P在![]() 上时,结论:PB﹣PA=
上时,结论:PB﹣PA=![]() PD.(证明方法类似②).
PD.(证明方法类似②).



科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,E是AD边上一动点,AE=m,将△ABE沿BE折叠后得到△GBE.延长BG交直线CD于点F.

(1)若∠ABE:∠BFC=n,则n= ______ ;
(2)当E运动到AD中点时,求线段GF的长;
(3)若限定F仅在线段CD上(含端点)运动,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,AB=2,点C在![]() 上运动,且∠ACB=30°.
上运动,且∠ACB=30°.

(1)求⊙O的半径;
(2)设点C到直线AB的距离为x,图中阴影部分的面积为y,求y与x之间的函数关系,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图①,请直接写出AE与DF的数量关系______________;
②将△EBF绕点B逆时针旋转到图②所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
(2)如图③,若四边形ABCD为矩形,BC=mAB,其他条件都不变,将△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图③中画出草图,并求出AE′与DF′的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com