
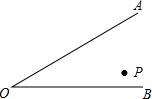
 如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P1、P2分别在OA、OB上,求作点P1、P2,使△PP1P2的周长最小,连接OP,若OP=10cm,求△PP1P2的周长.
如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P1、P2分别在OA、OB上,求作点P1、P2,使△PP1P2的周长最小,连接OP,若OP=10cm,求△PP1P2的周长. 分析 分别作点P关于OA、OB的对称点M、N,连接MN,分别交OA、OB于点P1、P2,连接OM、ON、PP1、PP2,根据轴对称的性质可得∴∠MOA=∠AOP,∠NOB=∠BOP,PP1=P1M,PP2=P2N,MO=PO=NO,从而求出△OMN是等边三角形△PP1P2的周长等于MN,从而得解.
解答 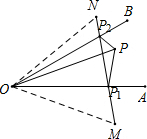 解:分别作点P关于OA、OB的对称点M、N,连接MN,分别交OA、OB于点P1、P2,连接OM、ON、PP1、PP2,此时△PP1P2的周长最小,△PP1P2的周长=P1P2,PP1+P1P2+PP2=MP1+P1P2+NP2=MN,
解:分别作点P关于OA、OB的对称点M、N,连接MN,分别交OA、OB于点P1、P2,连接OM、ON、PP1、PP2,此时△PP1P2的周长最小,△PP1P2的周长=P1P2,PP1+P1P2+PP2=MP1+P1P2+NP2=MN,
∵M、N分别是P关于OA、OB的对称点,
∴∠MOA=∠AOP,∠NOB=∠BOP,PP1=P1M,PP2=P2N,MO=PO=NO,
∴∠MON=∠MOA+∠AOP+∠NOB+∠BOP=2∠AOB,
∵∠AOB=30°,
∴∠MON=2×30°=60°,
∴△OMN是等边三角形,
又∵△PP1P2的周长=P1P2,PP1+P1P2+PP2=MP1+P1P2+NP2=MN,
∴△MNP的周长=MN=MO=PO=10cm.
点评 本题考查了轴对称的性质,等边三角形的判定与性质,熟记性质得到相等的边与角是解题的关键.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com