
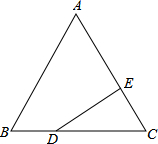
 等边△ABC中,BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,求证:DE⊥AC.
等边△ABC中,BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,求证:DE⊥AC. 分析 首先过点B作BF⊥AC交AC于点F,根据BF⊥AC,△ABC是等边三角形,可得点F是AC的中点;然后判断出$\frac{CE}{CF}=\frac{CD}{BC}$,即可推得DE∥BF,再根据BF⊥AC,推得DE⊥AC即可.
解答 证明:如图1,过点B作BF⊥AC交AC于点F,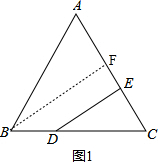 ,
,
∵BF⊥AC,△ABC是等边三角形,
∴点F是AC的中点,
∵BD=$\frac{1}{3}$BC,
∴CD=$\frac{2}{3}$BC,
∴$\frac{CD}{BC}=\frac{2}{3}$;
∵CE=$\frac{1}{3}$AC,
∴$\frac{CE}{CF}=\frac{\frac{1}{3}AC}{\frac{1}{2}AC}=\frac{2}{3}$,
∵$\frac{CD}{BC}=\frac{2}{3}$,
∴$\frac{CE}{CF}=\frac{CD}{BC}$,
∴DE∥BF,
又∵BF⊥AC,
∴DE⊥AC.
点评 此题还考查了等边三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:①等边三角形的内角都相等,且为60度;②等边三角形每条边上的中线、高线和所对角的平分线互相重合.③等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高或所对角的平分线所在的直线.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P1、P2分别在OA、OB上,求作点P1、P2,使△PP1P2的周长最小,连接OP,若OP=10cm,求△PP1P2的周长.
如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P1、P2分别在OA、OB上,求作点P1、P2,使△PP1P2的周长最小,连接OP,若OP=10cm,求△PP1P2的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
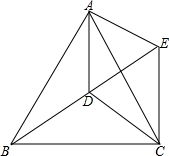 如图所示,点D是等边三角形ABC内一点,DA=13,DB=19,DC=21,将△ABD绕点A逆时针旋转到△ACE的位置,求△DEC的周长.
如图所示,点D是等边三角形ABC内一点,DA=13,DB=19,DC=21,将△ABD绕点A逆时针旋转到△ACE的位置,求△DEC的周长.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:解答题
如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。
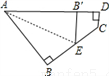
(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:填空题
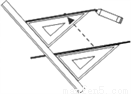
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
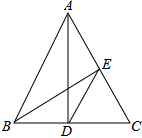 已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.
已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com