
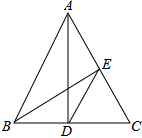
 已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.
已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④. 分析 利用三角形面积以及锐角三角函数关系和三角形中位线定理分别分析得出即可.
解答 解:∵AD⊥BC于D,BE⊥AC于E,
∴$\frac{1}{2}$BE•AC=$\frac{1}{2}$AD•BC,
∴BE•AC=AD•BC,
∴$\frac{AC}{BC}$=$\frac{AD}{BE}$,
故①正确;
无法得出AE•BE=AD•BD,故②错误;
∵∠C=60°,AD⊥BC于D,BE⊥AC于E,
∴cosC=$\frac{CD}{AC}$=$\frac{EC}{BC}$,
∴$\frac{CD}{CE}$=$\frac{AC}{BC}$,故③正确;
由AD⊥BC,BE⊥AC可得∠CEB=∠CDA=90°,∠C=∠C,
所以△CAD∽△CBE,
则$\frac{CE}{BC}$=$\frac{CD}{AC}$
所以△CDE∽△CAB,
所以$\frac{CD}{CA}$=$\frac{CE}{BC}$=$\frac{DE}{AB}$,
又因为∠C=60°,
所以CE:CB=1:2,
所以AB=2DE,故④正确.
故答案为:①③④.
点评 此题主要考查了三角形面积以及锐角三角函数关系和三角形中位线定理等知识,正确利用比例式的性质是解题关键.


科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
在平面直角坐标系中,已知反比例函数y=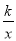 的图象经过点A(1,
的图象经过点A(1, 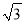 ).
).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线OA绕O点顺时针旋转30°得到线段OB,判断点B(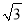 ,1)是否在此反比例函数的图象上,并说明理由.
,1)是否在此反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com