
【题目】如图,四边形ABCD是正方形,G是直线BC上的任意一点,DE⊥直线AG于点E.BF⊥直线AG于点F.
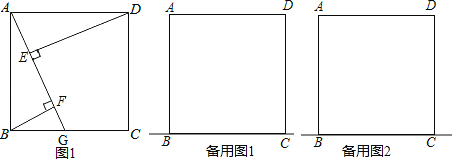
(1)如图1,若点G在线段BC上,判断AF,BF,EF之间的数量关系,并说明理由.
(2)若点G在CB延长线上,直接写出AF,BF,EF之间的数量关系.
(3)若点G在BC延长线上,直接写出AF,BF,EF之间的数量关系.
【答案】(1)AF=EF+BF.理由见解析;(2)AF+EF=BF;(3)AF+BF=EF.
【解析】
(1)证明△BAF≌△ADE即可.
(2)与(1)一样,都是证明△BAF≌△ADE即可.
(3)与(1)一样,都是证明△BAF≌△ADE即可.
(1)如图1,AF=EF+BF.
理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵DE⊥AG,BF⊥AG,
∴∠AFB=∠DEA=90°,
又∵∠BAF+∠DAE=∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中:
∴△BAF≌△ADE(AAS),
∴AE=BF,
∴AF=AE+EF=BF+EF.
(2)如图2,AF+EF=BF.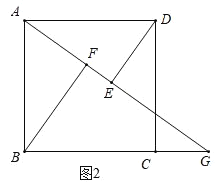
理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵DE⊥AG,BF⊥AG,
∴∠AFB=∠DEA=90°,
又∵∠BAF+∠DAE=∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中: ,
,
∴△BAF≌△ADE(AAS),
∴AE=BF,
∴AF+EF=AE=BF.
(3)如图3,AF+BF=EF.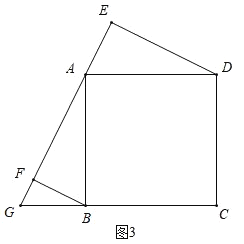
理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵DE⊥AG,BF⊥AG,
∴∠AFB=∠DEA=90°,
又∵∠BAF+∠DAE=∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中: ,
,
∴△BAF≌△ADE(AAS),
∴AE=BF,
∴EF=AE+AF=BF+AF.


科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
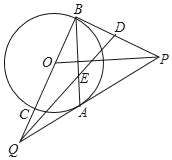
【题目】如图,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O上一点,且PA=PB,延长BO分别与⊙O、切线PA相交于C、Q两点.
(1)求证:PB是⊙O的切线;
(2)QD为PB边上的中线,若AQ=4,CQ=2,求QD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
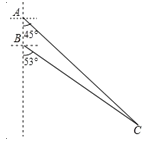
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
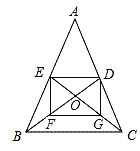
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com