
���� ��1�����ݵ�ƽ������Ҽӣ��ɵô𰸣�
��2������ͼ��ƽ������Ҽ����ɵô𰸣�
��3������ͼ���ƽ�ƹ��ɣ��ɵô𰸣�
��� �⣺��1����ͼ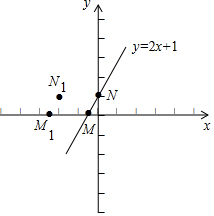 ��
��
M1��N1������ֱ�Ϊ��-$\frac{5}{2}$��0����-2��1����
��2���Ѻ���ͼ���ϵ����е㶼��x�᷽������ƽ��2����λ���õ���ͼ����һ��ֱ�ߣ�����ʽΪy=2x+5��
��3��y=kx+b��k��0����������ͼ����x�᷽������ƽ��2����λ����д����ͼ��ĺ�������ʽy=kx+2k+b��
���� ���⿼����һ�κ���ͼ���뼸�α任������ƽ�ƹ����ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
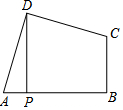 ��ͼ�������Ϊ16���ı���ABCD�У���ADC=��ABC=90�㣬AD=CD��DP��AB�ڵ�P����DP�ij���4��
��ͼ�������Ϊ16���ı���ABCD�У���ADC=��ABC=90�㣬AD=CD��DP��AB�ڵ�P����DP�ij���4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
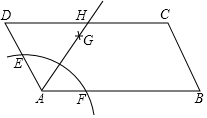 ��ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�һ����Ϊ�뾶��Բ�����ֱ�AD��AB�ڵ�E��F���ٷֱ��Ե�E��FΪԲ�ģ�����$\frac{1}{2}$EF�ij�Ϊ�뾶�������������ڵ�G��������AG������CD�ڵ�H����AB=6��AD=4�����ı���ABCH���ܳ���������ADH���ܳ�֮��Ϊ��������
��ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�һ����Ϊ�뾶��Բ�����ֱ�AD��AB�ڵ�E��F���ٷֱ��Ե�E��FΪԲ�ģ�����$\frac{1}{2}$EF�ij�Ϊ�뾶�������������ڵ�G��������AG������CD�ڵ�H����AB=6��AD=4�����ı���ABCH���ܳ���������ADH���ܳ�֮��Ϊ��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
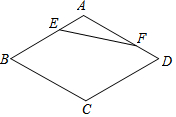 ��ͼ��������ABCD�У���B=60�㣬AB=a����E��F�ֱ��DZ�AB��AD�ϵĶ��㣬��AE+AF=a�����߶�EF����СֵΪ��������
��ͼ��������ABCD�У���B=60�㣬AB=a����E��F�ֱ��DZ�AB��AD�ϵĶ��㣬��AE+AF=a�����߶�EF����СֵΪ��������| A�� | 2$\sqrt{3}$a | B�� | $\frac{\sqrt{3}}{2}$a | C�� | $\sqrt{3}$a | D�� | $\frac{a}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
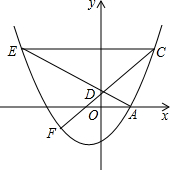 ��ͼ��������y=$\frac{1}{4}$x2+$\frac{1}{2}$x-2��x�������ύ�ڵ�A����D��0��m��Ϊy����������һ�㣬����AD���ӳ����������ڵ�E������C��4��n�����������ϣ���CE��x�ᣮ
��ͼ��������y=$\frac{1}{4}$x2+$\frac{1}{2}$x-2��x�������ύ�ڵ�A����D��0��m��Ϊy����������һ�㣬����AD���ӳ����������ڵ�E������C��4��n�����������ϣ���CE��x�ᣮ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
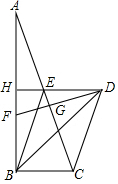 ��ͼ����Rt��ABC�У���ABC=90�㣬DH��ֱƽ��AB��AC�ڵ�E������BE��CD��CD=CE����F��AB�ϣ�BF=BC������BD��BDƽ�֡�ABC��
��ͼ����Rt��ABC�У���ABC=90�㣬DH��ֱƽ��AB��AC�ڵ�E������BE��CD��CD=CE����F��AB�ϣ�BF=BC������BD��BDƽ�֡�ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
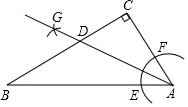 ��ͼ���ڡ�ABC�У���C=90�㣬AB=8��AC=4���Ե�AΪԲ�ģ�С��AC��Ϊ�뾶�������ֱ�AB��AC�ڵ�E��F���ٷֱ��Ե�E��FΪԲ�ģ�����EF��Ϊ�뾶�������������ڵ�G��������AG����BC�ڵ�D����D��AB�ľ���Ϊ��������
��ͼ���ڡ�ABC�У���C=90�㣬AB=8��AC=4���Ե�AΪԲ�ģ�С��AC��Ϊ�뾶�������ֱ�AB��AC�ڵ�E��F���ٷֱ��Ե�E��FΪԲ�ģ�����EF��Ϊ�뾶�������������ڵ�G��������AG����BC�ڵ�D����D��AB�ľ���Ϊ��������| A�� | 2 | B�� | 4 | C�� | $\frac{4\sqrt{3}}{3}$ | D�� | $\frac{2\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com