【题目】刘明上周末买进某只股票2000股，每股38元，下表为本周内每日该股票的涨跌情况（单位：元）
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 | +2.1 | +1.5 | -2 | -1 | +3.8 | -2.7 |
（1）星期三收盘时，每股是多少元？
（2）本周内最高价是每股多少元？最低每股多少元？
（3）已知买进股票时付了1.5‰的手续费，卖出时需付成交额1.5‰的手续费和1‰的交税，刘明周六收盘前全部卖出股票获利多少？
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（-4, 1），B（-1,3），C（-1,1）
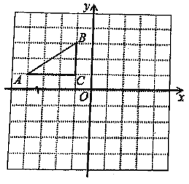
（1）将△ABC以原点O为旋转中心旋转180°，画出旋转后对应的△
;平移△ABC，若A对应的点
坐标为（-4，-5），画出△
;
（2）若△绕某一点旋转可以得到△，直接写出旋转中心坐标是__________;
（3）在x轴上有一点P是的PA+PB的值最小，直接写出点P的坐标___________;
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国是世界上严重缺水的国家之一．为了倡导“节约用水从我做起”，小刚在他所在班的50名同学中，随机调查了10名同学家庭中一年的月均用水量（单位：t），并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数；
【2】根据样本数据，估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在ABCD中，点E是BC的中点，连接AE并延长交DC的延长线于点F，连接BF．
(1)求证：△ABE≌△FCE；
(2)若AF＝AD，求证：四边形ABFC是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在等腰梯形ABCD中，AD//BC，E是AB的中点，过点E作EF//BC交CD于点F，AB＝4，BC＝6，∠B＝60°．
（1）求点E到BC的距离；
（2）点P为线段EF上的一个动点，过点P作PM⊥EF交BC于M，过M作MN//AB交折线ADC于N，连结PN，设EP＝x．
①当点N在线段AD上时（如图2），△PMN的形状是否发生改变？若不变，求出△PMN的周长；若改变，请说明理由；
②当点N在线段DC上时（如图3），是否存在点P，使△PMN为等腰三角形？若存在，请求出所有满足条件的x的值；若不存在，请说明理由．
图1 图2 图3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法中，正确的个数有（ ）
①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为
；
②直角三角形的最大边长为
，最短边长为1，则另一边长为
；
③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；
④等腰三角形面积为12，底边上的高为4，则腰长为5．
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知数轴上的A、B两点分别对应数字a、b，且a、b满足|4a-b|+（a-4）2=0
（1）a= ，b= ，并在数轴上面出A、B两点；
（2）若点P从点A出发，以每秒3个单位长度向x轴正半轴运动，求运动时间为多少时，点P到点A的距离是点P到点B距离的2倍；
（3）数轴上还有一点C的坐标为30，若点P和点Q同时从点A和点B出发，分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动，P点到达C点后，再立刻以同样的速度返回，运动到终点A．求点P和点Q运动多少秒时，P、Q两点之间的距离为4，并求此时点Q对应的数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，PA为⊙O的切线，A为切点。过A作OP的垂线AB，垂足为点C，交⊙O于点B。延长BO与⊙O交于点D，与PA的延长线交于点E。
（1）求证：PB为⊙O的切线；
（2）试探究线段AD、AB、CP之间的等量关系，并加以证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
