
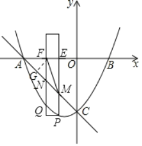
����Ŀ����ͼ��������y��![]() x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B������Ϊ��3��0������C������Ϊ��0����5������һ����Ϊ1�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��AC�ڵ�M�͵�N����x���ڵ�E�͵�F��
x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B������Ϊ��3��0������C������Ϊ��0����5������һ����Ϊ1�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��AC�ڵ�M�͵�N����x���ڵ�E�͵�F��
��1���������ߵĽ���ʽ����A�����ꣻ
��2������M��N�����߶�AC��ʱ������MF�����sin��AMF��![]() �����Q�����ꣻ
�����Q�����ꣻ
��3���ھ��ε�ƽ�ƹ����У��Ƿ�����Ե�P��Q��M��NΪ������ı�����ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��y��![]() x2+
x2+![]() x��5��A����5��0������2��Q���꣨��4����
x��5��A����5��0������2��Q���꣨��4����![]() ������3�����ڣ���M������Ϊ����2����3����2+
������3�����ڣ���M������Ϊ����2����3����2+![]() ����3��
����3��![]() ����2��
����2��![]() ����3+
����3+![]() ����
����
��������
��1������B�����ꡢ��C������ֱ���뺯������ʽ���b��c��ֵ����������߽���ʽ��õ�A�����ꣻ
��2����FG��AC��G�����F���꣨m��0��������sin��AMF=![]() ���г����̼��ɽ�����⣮
���г����̼��ɽ�����⣮
��3�����ٵ�MN�ǶԽ���ʱ�����F��m��0������QN=PM���г����̼��ɽ�����⣮�ڵ�MNΪ��ʱ�����Q��m��![]() m2+
m2+![]() m-5�����P��m+1��
m-5�����P��m+1��![]() m2+
m2+![]() m-6�������������߽���ʽ���ⷽ�̼��ɣ�
m-6�������������߽���ʽ���ⷽ�̼��ɣ�
��1�����������ϵĵ�B������Ϊ��3��0������C������Ϊ��0����5��
�ཫ�����y�T![]() x2+bx+c����
x2+bx+c����![]() ��
��
���b��![]() ��c����5��
��c����5��
�������ߵĽ���ʽΪy��![]() x2+
x2+![]() x��5��
x��5��
��y=0�ɵ�x=3��-5
���A�������ǣ���5��0����
��2����FG��AC��G�����F���꣨m��0����
��AF��m+5��AE��EM��m+6��FG��![]() ��m+5����FM��
��m+5����FM��![]() ��
��
��sin��AMF��![]() ��
��
��![]() ��
��
��![]() ��
��
�����õ�2m2+19m+44��0��
�ࣨm+4����2m+11����0��
��m����4��5.5����������
���Q���꣨��4����![]() ����
����
��3���ٵ�MN�ǶԽ���ʱ����M��y����Ҳ࣬���F��m��0����
��ֱ��AC����ʽΪy����x��5��
���N��m����m��5������M��m+1����m��6����
��QN��PM��
�ੁm��5����![]() m2+
m2+![]() m��5����[
m��5����[![]() ��m+1��2+
��m+1��2+![]() ��m+1����5]������m��6����
��m+1����5]������m��6����
���m����3+![]() ��3��
��3��![]() ����������
����������
��ʱM����2+![]() ����3��
����3��![]() ����
����
��MN�ǶԽ���ʱ����N�ڵ�A�����ʱ�����F��m��0����
�ࣨ![]() m2+
m2+![]() m��5��������m��5��������m��6����[
m��5��������m��5��������m��6����[![]() ��m+1��2+
��m+1��2+![]() ��m+1����5]��
��m+1����5]��
���m����3��![]() ��3+
��3+![]() ����������
����������
��ʱM����2��![]() ����3+
����3+![]() ����
����
�ڵ�MNΪ��ʱ�����Q��m��![]() m2+
m2+![]() m��5�����P��m+1��
m��5�����P��m+1��![]() m2+
m2+![]() m��6����
m��6����
��NQ��PM��
��![]() m2+
m2+![]() m��6��
m��6��![]() ��m+1��2+
��m+1��2+![]() ��m+1����5
��m+1����5
���m����3��
���M���꣨��2����3����
�����������Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ����M������Ϊ����2����3����2+![]() ����3��
����3��![]() ����2��
����2��![]() ����3+
����3+![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η�����ʵ������Ϊ��4���ǣ� ��
A. x2+2x��4=0 B. x2��4x+4=0 C. x2+4x+10=0 D. x2+4x��5=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
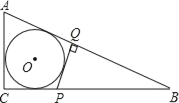
����Ŀ����ͼ����O������Rt��ABC����P����Q�ֱ���ֱ�DZ�BC��б��AB�ϣ�PQ��AB����PQ���O���У���AC��2PQ����tan��B��ֵΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y��mx2+��5m+3��x+4m��mΪ������m��0������������˵����
�ٲ���mΪ��ֵ������ͼ��һ�������㣨��1����3����
�ڵ�m����1ʱ������ͼ������������3�����㣻
�۵�m��0��x�ݩ�![]() ʱ������y��x���������С���ж���٣���˵�����ɣ�
ʱ������y��x���������С���ж���٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
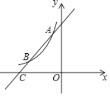
����Ŀ����֪һ�κ���y��x+4ͼ���뷴��������y��![]() ��k��0��ͼ����A����1��a����B���㣮
��k��0��ͼ����A����1��a����B���㣮
��1����˷����������ı���ʽ��
��2����x+4��![]() �����ú���ͼ����x��ȡֵ��Χ��
�����ú���ͼ����x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
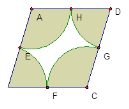
����Ŀ����ͼ������ABCD���߳�����2����E��F��G��H�ֱ���AB��BC��CD��DA���е㣬ͼ����Ӱ�������ĸ�С������ɣ����������ж�����ȷ���У� ��
�ٿհ�ͼ�οհײ��ֵ��ܳ�=2![]() �ڿհײ��ֵ����=
�ڿհײ��ֵ����=![]()
���ĸ�С���ε������ =![]() �����ε����=4
��������=4
A 1�� B 2�� C 3�� D 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪֱ�������Σ���C=90�㣬BC=2cm����A=30�����ı���DEFGΪ���Σ�DE=2![]() cm��EF=6cm���ҵ�C��B��E��F��ͬһ��ֱ���ϣ���B���E�غϣ�Rt��ABC��ÿ��1cm���ٶ��ؾ���DEFG�ı�EF����ƽ�ƣ�����C���F�غ�ʱֹͣ����Rt��ABC�����DEFG���ص����ֵ����Ϊycm2���˶�ʱ��xs���ܷ�ӳycm2��xs֮�亯����ϵ�Ĵ���ͼ���ǣ�������
cm��EF=6cm���ҵ�C��B��E��F��ͬһ��ֱ���ϣ���B���E�غϣ�Rt��ABC��ÿ��1cm���ٶ��ؾ���DEFG�ı�EF����ƽ�ƣ�����C���F�غ�ʱֹͣ����Rt��ABC�����DEFG���ص����ֵ����Ϊycm2���˶�ʱ��xs���ܷ�ӳycm2��xs֮�亯����ϵ�Ĵ���ͼ���ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
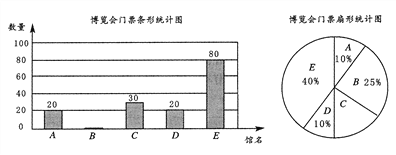
����Ŀ��ij��˾��֯����Ա����һ�������A��B��C��D��E���չ�ݲιۣ���˾������Ʊ���ࡢ�������Ƴɵ����κ�����ͳ��ͼ��ͼ��ʾ�� �����ͳ��ͼ�ش��������⣺
��1��������ͳ��ͼ������ͳ��ͼ��ͼ�в���������
��2����![]() ����Ʊ��ʣ��һ�ţ���Ա��С����С������Ҫ�����Ǿ������ó��˿��Ƶķ�����ȷ���������ǣ�����ͬһ����������ֱ��������1��2��3��4��������ϴ�Ⱥ��泯�Ϸ����������ϣ�ÿ�������һ����һ��ֻ��һ�ţ�һ�˳��������֣����Ż�������һ�˳飮��С����õ����ֱ�С����õ����ִ���Ʊ��С���������С������ ���û���״ͼ���б��ķ��������С����С�������Ʊ�ĸ��ʣ���˵����������˫���Ƿ�ƽ��
����Ʊ��ʣ��һ�ţ���Ա��С����С������Ҫ�����Ǿ������ó��˿��Ƶķ�����ȷ���������ǣ�����ͬһ����������ֱ��������1��2��3��4��������ϴ�Ⱥ��泯�Ϸ����������ϣ�ÿ�������һ����һ��ֻ��һ�ţ�һ�˳��������֣����Ż�������һ�˳飮��С����õ����ֱ�С����õ����ִ���Ʊ��С���������С������ ���û���״ͼ���б��ķ��������С����С�������Ʊ�ĸ��ʣ���˵����������˫���Ƿ�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
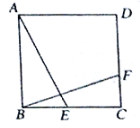
����Ŀ����ͼ,������![]() ��,��
��,��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() ��, ����
��, ����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��, ����
��, ����![]() ,��
,��![]() ,��
,��![]() ___.
___.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com