
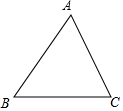
 如图,△ABC中,AB=AC,∠BAC=80°,则∠ABC的平分线与△ABC的一条外角平分线所夹的角(不包括钝角)为25°或40°.
如图,△ABC中,AB=AC,∠BAC=80°,则∠ABC的平分线与△ABC的一条外角平分线所夹的角(不包括钝角)为25°或40°. 分析 ∠CAE、∠ACF分别为△ABC的外角,AM平分∠CAE、CN平分∠ACF,当∠ABC的平分线交AM于点M,利用外角的性质及角平分线的定义可求得∠AMB,当∠ABC的平分线交CN于点N,同理可求得∠BNC,则可求得答案.
解答 解:
设∠ABC的角平分线为BD,∠CAE、∠ACF分别为△ABC的外角,AM平分∠CAE、CN平分∠ACF,
①当∠ABC的平分线交AM于点M,如图1,
∵∠BAC=80°,
∴∠EAC=100°,
∵AM平分∠EAC,
∴∠EAM=50°,
∵AB=AC,
∴∠ABC=50°,
∵BM平分∠ABC,
∴∠ABM=25°,
∴∠AMB=∠EAM-∠ABM=50°-25°=25°;
②当∠ABC的平分线交CN于点N,如图2,
∵∠BAC=80°,AB=AC,
∴∠ABC=50°,∠ACF=130°,
∵BN、CN为角平分线,
∴∠CBN=25°,∠FCN=65°,
∵∠FCN=∠BNC+∠CBN,
∴∠BNC=65°-25°=40°;
综上可知∠ABC的平分线与△ABC的一条外角平分线所夹的角为25°或40°,
故答案为:25°或40°.
点评 本题主要考查等腰三角形的性质,根据题意分别画出两种图形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 8.01346 | B. | 8.0134×106 | C. | 8.0134×107 | D. | 8.0134×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
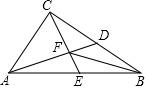 如图,在Rt△ABC中,∠ACB=90°,AD、CE分别是BC、AB边上的中线,且满足AD⊥CE,垂足为F,联结BF.
如图,在Rt△ABC中,∠ACB=90°,AD、CE分别是BC、AB边上的中线,且满足AD⊥CE,垂足为F,联结BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,AB,CD相交于点O,AE为∠BAD的平分线,CE为∠BCD的平分线.
如图所示,AB,CD相交于点O,AE为∠BAD的平分线,CE为∠BCD的平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com