
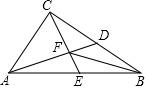
 如图,在Rt△ABC中,∠ACB=90°,AD、CE分别是BC、AB边上的中线,且满足AD⊥CE,垂足为F,联结BF.
如图,在Rt△ABC中,∠ACB=90°,AD、CE分别是BC、AB边上的中线,且满足AD⊥CE,垂足为F,联结BF.分析 (1)根据已知条件得到∠AFC=∠AFE=∠ACD=90°,推出△AFC∽△ACD;同理△CDF∽△ACD,根据相似三角形的性质得到∠ACE=∠ADC,根据直角三角形的性质得到CE=AE=BE=$\frac{1}{2}$AB,根据等腰三角形的性质得到∠CAE=∠ACE,求得∠CAE=∠ADC,于是得到△BAC∽△ADC;
(2)根据相似三角形的性质得到$\frac{CD}{AD}=\frac{DF}{CD}$,等量代换得到$\frac{BD}{AD}=\frac{DF}{BD}$,推出△BDF∽△ADB,于是得到结论.
解答 解:(1)与△ACD相似的三角形有△ACF,△CDF,△ABC
∵在Rt△ABC中,∠ACB=90°,AD⊥CE,
∴∠AFC=∠AFE=∠ACD=90°,
∵∠CAD=∠FAC,
∴△AFC∽△ACD;同理△CDF∽△ACD,
∴∠ACE=∠ADC,
∵CE是中线,
∴CE=AE=BE=$\frac{1}{2}$AB,
∴∠CAE=∠ACE,
∴∠CAE=∠ADC,
∴△BAC∽△ADC;
(2)∵△CDF∽△DAC,
∴$\frac{CD}{AD}=\frac{DF}{CD}$,
∵AD是BC边上的中线,
∴CD=BD,
∴$\frac{BD}{AD}=\frac{DF}{BD}$,
∵∠BDF=∠ADB,
∴△BDF∽△ADB,
∴$\frac{BF}{AB}$=$\frac{BD}{AD}$.
点评 此题考查了相似三角形的判定与性质.注意掌握有两边对应成比例且夹角相等三角形相似是关键.


科目:初中数学 来源: 题型:解答题
 在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.
在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,P、Q、R是双曲线y=$\frac{k}{x}$(k<0)上的三点,过这三点分别作y轴的垂线,垂足分别是A、B、C,连OP、OQ、QR得到△POA、△QOB、△ROC,设它们的面积分别是S1、S2、S3,则S1、S2、S3大小关系是( )
如图,P、Q、R是双曲线y=$\frac{k}{x}$(k<0)上的三点,过这三点分别作y轴的垂线,垂足分别是A、B、C,连OP、OQ、QR得到△POA、△QOB、△ROC,设它们的面积分别是S1、S2、S3,则S1、S2、S3大小关系是( )| A. | S1<S2<S3 | B. | S2<S1<S3 | C. | S1<S3<S2 | D. | S1=S2=S3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | 2x+1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有理数包括正整数、零和负分数 | |
| B. | -a不一定是整数 | |
| C. | -5和+(-5)互为相反数 | |
| D. | 两个有理数的和一定大于每一个加数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com