
【题目】如图![]() ,一条笔直的公路上有
,一条笔直的公路上有![]() 、
、![]() 、
、![]() 三地
三地![]() 、
、![]() 两地相距
两地相距![]() 千米,甲、乙两个野外徒步爱好小组从
千米,甲、乙两个野外徒步爱好小组从 ![]() 、
、![]() 两地同时出发,沿公路始终匀速相向而行,分别走向
两地同时出发,沿公路始终匀速相向而行,分别走向![]() 、
、![]() 两地.甲、乙两组到
两地.甲、乙两组到![]() 地的距离
地的距离![]() ,
,![]() (千米)与行走时间
(千米)与行走时间![]() (时)的关系如图
(时)的关系如图![]() 所示.
所示.
(1)请在图![]() 中标出
中标出![]() 地的位置,并写出相应的距离:
地的位置,并写出相应的距离:![]()
![]() ;
;
(2)在图![]() 中求出甲组到达
中求出甲组到达![]() 地的时间
地的时间![]() ;
;
(3)求岀乙组从![]() 地到
地到![]() 地行走过程中
地行走过程中![]() 与行走时间
与行走时间![]() 的关系式.
的关系式.
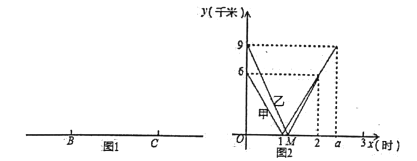
【答案】(1)9.(2)2.5.(3)y2=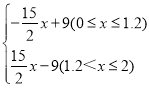 .
.
【解析】
(1)由图2可知AC=9km.画出图象即可.
(2)求出甲的速度即可解决问题.
(3)先求出点M坐标,再求出分段函数即可.
(1)A地的位置,如图所示,由题意AC=9km.
故答案为9.
![]()
(2)由图2可知,甲的速度为6km/h,所以甲组到达![]() 地的时间为
地的时间为![]() =2.5.
=2.5.
故a=2.5.
(3)由图2可知乙的速度为![]() =7.5km/h,
=7.5km/h,
∵![]() =1.2
=1.2
∴点M坐标(1.2,0),
当0≤x≤1.2时,设函数为y2=k1x+b1,
把(0,9),(1.2,0)代入y2=k1x+b1,
得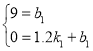 ,解得
,解得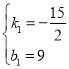
∴当0≤x≤1.2时,y2=-![]() x+9;
x+9;
当1.2<x≤2时,设函数为y2=k2x+b2,
把(2,6),(1.2,0)代入y2=k1x+b1,
得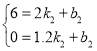 ,解得
,解得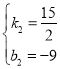
∴当1.2<x≤2时,y2=![]() x-9;
x-9;
综上y2=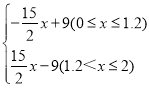 .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() 是郑州市二七区三个垃圾存放点,点
是郑州市二七区三个垃圾存放点,点![]() ,
,![]() 分别位于点
分别位于点![]() 的正北和正东方向,
的正北和正东方向,![]() 米,八位环卫工人分别测得的
米,八位环卫工人分别测得的![]() 长度如下表:
长度如下表:
甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
BC(单位:米) | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
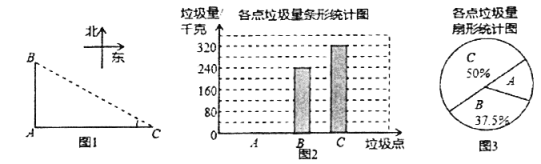
(1)求表中![]() 长度的平均数
长度的平均数![]() 、中位数、众数;
、中位数、众数;
(2)求![]() 处的垃圾量,并将图2补充完整;
处的垃圾量,并将图2补充完整;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步深化基教育课程改革,构建符合素质教育要求的学校课程体系,某学校自主开发了A书法、B阅读,C足球,D器乐四门校本选修课程供学生选择,每门课程被选到的机会均等.
(1)学生小红计划选修两门课程,请写出所有可能的选法;
(2)若学生小明和小刚各计划送修一门课程,则他们两人恰好选修同一门课程的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.

(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,![]() ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
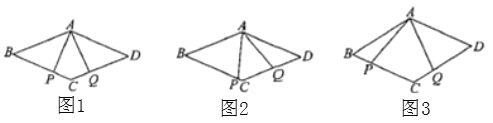
【题目】已知点![]() 分别在菱形
分别在菱形![]() 的边
的边![]() 上滑动(点
上滑动(点![]() 不与
不与![]() 重合),且
重合),且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 与
与![]() 不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
(3)如图3,若![]() ,请直接写出四边形
,请直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .过点
.过点![]() 且与直线
且与直线![]() 平行的直线交
平行的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
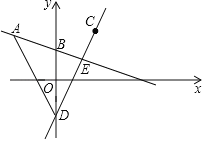
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com