
【题目】矩形ANCD中,AD=5,CD=3,在直线BC上取一点E,使△ADE是以DE为底的等腰三角形,过点D作直线AE的垂线,垂足为点F,则EF= .
【答案】9或1
【解析】解;如图1中, 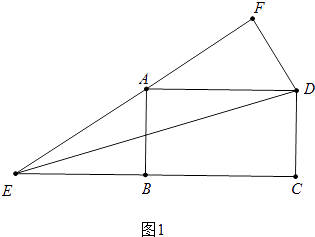
∵四边形ABCD是正方形,
∴AD=BC=5,AB=CD=3,∠ABC=∠C=∠ABE=90°,AD∥EC
∵AE=AD=5,
∴∠AED=∠ADE=∠DEC,
在RT△ABE中,∵AE=5,AB=3,
∴EB= ![]() =
= ![]() =4,
=4,
在△EDF和△EDC中,
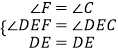 ,
,
△EDF≌△EDC
∴EF=EC=EB+BC=9.
如图2中, 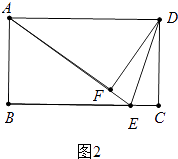
∵AD=AE=5,AB=3,
∴BE= ![]() =4,
=4,
∴EC=1,
∵AD∥BC,
∴∠ADE=∠DEC=∠AED,
在△EDF和△EDC中,
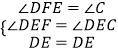 ,
,
∴△DEF≌△DEC,
∴EF=EC=1,
综上所述EF=9或1.
所以答案是9或1.
【考点精析】通过灵活运用等腰三角形的性质和勾股定理的概念,掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.


科目:初中数学 来源: 题型:
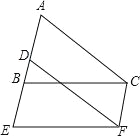
【题目】如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=______.
(3)若∠ABC=75°,求∠CFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
证明:∵∠1=∠2(已知),∠2=∠3(______)
∴∠1=∠3(______)
∴BD∥CE(______)
∴∠C=∠ABD(______)
又∵∠C=∠D(已知)
∴∠D=∠ABD(_______)
∴________(________)
∴∠A=∠F(________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胜利中学在一次健康知识竞赛活动中,抽取了一部分学生的测试成绩(成绩均为整数),整理后绘制成如图所示的频数直方图,根据图示信息,下列描述不正确的是( )
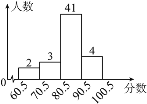
A. 抽查了50名学生
B. 成绩在60.5~70.5分范围的频数为2
C. 成绩在70.5~80.5分范围的频数比成绩在60.5~70.5分范围的频数多1
D. 成绩在70.5~80.5分范围的频率为0.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信部门计划修建一条连接B,C两地的电缆.测量人员在山脚A点测得B,C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?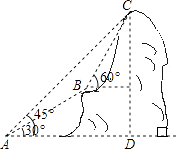
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年11月的最后一个星期四是感恩节,小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人.他将调查结果分为如下四类:A类﹣﹣当面致谢;B类﹣﹣打电话;C类﹣﹣发短信息或微信;D类﹣﹣写书信.他将调查结果绘制成如图不完整的扇形统计图和条形统计图:
请你根据图中提供的信息完成下列各题:
(1)补全条形统计图;
(2)在A类的同学中,有3人来自同一班级,其中有1人学过主持.现准备从他们3人中随机抽出两位同学主持感恩节主题班会课,请你用树状图或表格求出抽出的两人都没有学过主持的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com