
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
【答案】(1)共有三种方案:方案一:A产品18件,B产品12件,方案二:A产品19件,B产品11件,方案三:A产品20件,B产品10件;(2).
【解析】试题(1)根据两种产品所需要的甲、乙两种原料列出不等式组,然后求解即可;
(2)根据总利润等于两种产品的利润之和列式整理,然后根据一次函数的增减性求出最大利润即可.
试题解析:解:(1)根据题意得: ![]() ,解得18≤x≤20,∵x是正整数,∴x=18、19、20,共有三种方案:
,解得18≤x≤20,∵x是正整数,∴x=18、19、20,共有三种方案:
方案一:A产品18件,B产品12件,方案二:A产品19件,B产品11件,方案三:A产品20件,B产品10件;
(2)根据题意得:y=700x+900(30﹣x)=﹣200x+27000,∵﹣200<0,∴y随x的增大而减小,∴x=18时,y有最大值,y最大=﹣200×18+27000=23400元.
答:利润最大的方案是方案一:A产品18件,B产品12件,最大利润为23400元.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,点D在直角边BC上,DE平分∠ADB,∠1=∠2=∠3,AC=5cm.
(1)求∠3的度数;
(2)判断DE与AB的位置关系,并说明理由;
(3)求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图: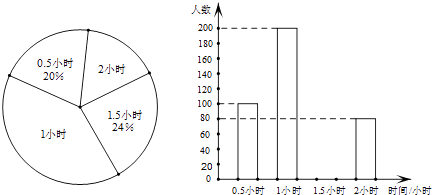
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A.![]()
B.2 ![]()
C.![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在五一期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位.
(1)求外出旅游的学生人数是多少,单租45座的客车需多少辆?
(2)已知45座的客车每辆租金250元,60座的客车每辆租金300元,为节省租金,并且保证每个学生都有座,决定同时租用两种客车,使得租车总数比单租45座的客车少一辆,问45座的客车和60座的客车分别租多少辆才能使得租金最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ANCD中,AD=5,CD=3,在直线BC上取一点E,使△ADE是以DE为底的等腰三角形,过点D作直线AE的垂线,垂足为点F,则EF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,c为斜边,a、b为直角边,则化简 ![]() 的结果为( )
的结果为( )
A.3a+b﹣c
B.﹣a﹣3b+3c
C.a+3b﹣3c
D.2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1 ,
(2)点C1的坐标是;
(3)以点B为位似中心,在网格内画出△A2B2C2 ,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com