
【题目】如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A.![]()
B.2 ![]()
C.![]()
D.3 ![]()
科目:初中数学 来源: 题型:
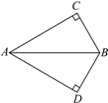
【题目】如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加的条件是________或________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).
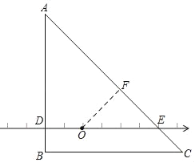
如图,等腰直角三角形ABC的一条直角边AB垂直数轴于点D,斜边AC与数轴交于点E,数轴上点O表示的有理数是0,若AB=BC=8,AD=6,OD=2.点O到边BC的距离与线段DB的长相等.
(1)求d(点O,点E);
(2)求d(点O,△ABC).
查看答案和解析>>
科目:初中数学 来源: 题型:
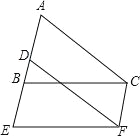
【题目】如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=______.
(3)若∠ABC=75°,求∠CFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
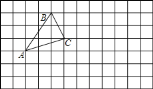
【题目】画图并填空:(每个小方格的边长为1)
(1)画出△ABC先向右平移6格,再向下平移2格得到的△A1B1C1.
(2)线段AA1与线段BB1的关系是: .
(3)△ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
证明:∵∠1=∠2(已知),∠2=∠3(______)
∴∠1=∠3(______)
∴BD∥CE(______)
∴∠C=∠ABD(______)
又∵∠C=∠D(已知)
∴∠D=∠ABD(_______)
∴________(________)
∴∠A=∠F(________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胜利中学在一次健康知识竞赛活动中,抽取了一部分学生的测试成绩(成绩均为整数),整理后绘制成如图所示的频数直方图,根据图示信息,下列描述不正确的是( )
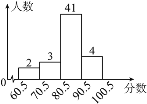
A. 抽查了50名学生
B. 成绩在60.5~70.5分范围的频数为2
C. 成绩在70.5~80.5分范围的频数比成绩在60.5~70.5分范围的频数多1
D. 成绩在70.5~80.5分范围的频率为0.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com