
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
【答案】
(1)解:A(﹣1,0),B(3,0),C(0,3).
抛物线的对称轴是:直线x=1.
(2)解:①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得: ![]()
解得: ![]() .
.
所以直线BC的函数关系式为:y=﹣x+3.
当x=1时,y=﹣1+3=2,
∴E(1,2).
当x=m时,y=﹣m+3,
∴P(m,﹣m+3).
在y=﹣x2+2x+3中,当x=1时,y=4.
∴D(1,4)
当x=m时,y=﹣m2+2m+3,
∴F(m,﹣m2+2m+3)
∴线段DE=4﹣2=2,
线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m
∵PF∥DE,
∴当PF=ED时,四边形PEDF为平行四边形.
由﹣m2+3m=2,
解得:m1=2,m2=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF与x轴交于点M, 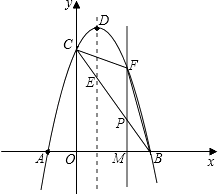
由B(3,0),O(0,0),
可得:OB=OM+MB=3.
∵S=S△BPF+S△CPF
即S= ![]() PFBM+
PFBM+ ![]() PFOM=
PFOM= ![]() PF(BM+OM)=
PF(BM+OM)= ![]() PFOB.
PFOB.
∴S= ![]() ×3(﹣m2+3m)=﹣
×3(﹣m2+3m)=﹣ ![]() m2+
m2+ ![]() m(0≤m≤3).
m(0≤m≤3).
∵B(3,0),C(0,3),D(1,4),
∴ ![]() ,
,
∴ ![]() ,
,
∵∠DEC=∠COB=90°,
∴△DEC∽△COB,
∴∠DCE=∠CBO,
∴∠DCE+∠OCB=90°,
∴DC⊥BC,
∴△BCD的外接圆圆心M为BD中点, 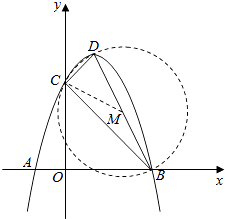
∴MX= ![]() =2,MY=
=2,MY= ![]() =2,
=2,
∴△BCD的外接圆圆心M(2,2)
【解析】(1)与x轴交点令y=0,解方程即可,与y轴交点,令x=0,求出y即可,对称轴可套公式x=![]() ;(2)若四边形PEDF为平行四边形,可得PF∥DE,PF=ED,用m的代数式表示PF,等于DE的长,构建方程即可;(3)用分割的方法把三角形面积分成S△BPF+S△CPF,分别用m的代数式表示底边和高即可.
;(2)若四边形PEDF为平行四边形,可得PF∥DE,PF=ED,用m的代数式表示PF,等于DE的长,构建方程即可;(3)用分割的方法把三角形面积分成S△BPF+S△CPF,分别用m的代数式表示底边和高即可.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A.![]()
B.2 ![]()
C.![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1 ,
(2)点C1的坐标是;
(3)以点B为位似中心,在网格内画出△A2B2C2 ,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
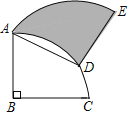
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )
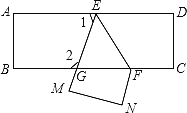
A. 115°B. 125°C. 135°D. 145°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com