
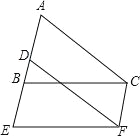
【题目】如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=______.
(3)若∠ABC=75°,求∠CFE的度数.
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三个点对应的数分别是a、b、c,且满足|a+24|+|b+10|+(c-10)2=0;动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
![]()
(1)求a、b、c的值;
(2)若点P到A点距离是到B点距离的2倍,求点P的对应的数;
(3)当点P运动到B点时,点Q从A点出发,以每秒2个单位的速度向C点运动,Q点到达C点后.再立即以同样的速度返回,运动到终点A,在点Q开始运动后第几秒时,P、Q两点之间的距离为8?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.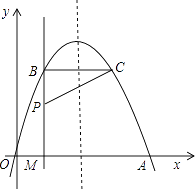
(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图: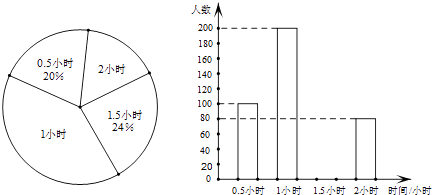
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于分式的判断,正确的是( )
A.当x=2时, ![]() 的值为零
的值为零
B.无论x为何值, ![]() 的值总为正数
的值总为正数
C.无论x为何值, ![]() 不可能得整数值
不可能得整数值
D.当x≠3时, ![]() 有意义
有意义
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A.![]()
B.2 ![]()
C.![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ANCD中,AD=5,CD=3,在直线BC上取一点E,使△ADE是以DE为底的等腰三角形,过点D作直线AE的垂线,垂足为点F,则EF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com