

���� ��1���������E��D��C�����꣬�����ô���ϵ������⼴�ɣ�
��2����t��ʾ����G��Q���꣺OG=t��G��t��0����Q��t��$-\frac{5}{6}$t2+$\frac{13}{6}$t+1��������t��ʾ�߶�GP��QP��GP=$\frac{2}{5}$+t��QP=$-\frac{5}{6}$t2+$\frac{13}{6}$t+1-��$\frac{2}{5}$+t��=$-\frac{5}{6}$t2+$\frac{7}{6}$t+$\frac{3}{5}$����N��F��P��QΪ����Ķ������һ�����Σ��ٸ��������ʽ�����г�������ϵʽ��
�����ö��κ����Ķ��㹫ʽ�����������ʱ��t��ֵ��
��3�������ת180���֪ʶ���C2�Ľ���ʽ����y=0�����x�ύ�����꣬�����K�������꣬��ʾ����DSK��������������������6��������⣮
��� �⣺�ɾ���OABC�ı�OA=3��OC=3��
���A��0��2������C��3��0������AOC=90�㣬��OAB=90�㣬AB=OC=3��BC=OA=2��
��ODƽ�֡�AOC��
���AOD=45�㣬
���OBA=45��
��AD=0A=2��BD=AB-AD=3-2=1��
���D��2��2��
��DE��DC��
���ADE+��BDC=90�㣬
�֡ߡ�BDC+��BCD=90�㣬
���ADE=��BCD��
�ߡ�CBD=��DAE=90�㣬AD=BC=2��
�ڡ�AED�͡�BDC�У�
$\left\{\begin{array}{l}{��CBD=��DAE}\\{AD=BC}\\{��ADE=��BCD}\end{array}\right.$
���AED�ա�BDC��SAS����
��AE=BD=1
���E��0��1��
��1���������߽���ʽΪ��y=ax2+bx+c��
��E��0��1����D��2��2����C��3��0���������ã�1=c�� 2=4a+2b+c�� 0=9a+3b+c��
��ã�a=$-\frac{5}{6}$��b=$\frac{13}{6}$��c=1��
���ԣ�����E��D��C�������ߵĽ���ʽΪ��y=$-\frac{5}{6}$x2+$\frac{13}{6}$x+1��
��2����
y=$-\frac{5}{6}$x2+$\frac{13}{6}$x+1����y=0ʱ��0=$-\frac{5}{6}$x2+$\frac{13}{6}$x+1����ã�x1=3��x2=$-\frac{2}{5}$��
��G��$-\frac{2}{5}$��0����OG=$\frac{2}{5}$��
��F��$-\frac{7}{5}$��0���ã�OF=$\frac{7}{5}$��FN=OF=$\frac{7}{5}$��FG=$-\frac{2}{5}$-��$-\frac{7}{5}$��=1
��G����ԭ��O����˶�ʱ��Ϊtʱ��OG=t��G��t��0����GP=$\frac{2}{5}$+t
��x=tʱ��y=$-\frac{5}{6}$t2+$\frac{13}{6}$t+1
��Q��t��$-\frac{5}{6}$t2+$\frac{13}{6}$t+1����
��QP=$-\frac{5}{6}$t2+$\frac{13}{6}$t+1-��$\frac{2}{5}$+t��=$-\frac{5}{6}$t2+$\frac{7}{6}$t+$\frac{3}{5}$
S=��NF+QP����FG��$\frac{1}{2}$
S=��$\frac{7}{5}$+$-\frac{5}{6}$t2+$\frac{7}{6}$t+$\frac{3}{5}$����1��$\frac{1}{2}$
S=$-\frac{5}{12}$t2+$\frac{7}{12}$t+1
��S=$-\frac{5}{12}$t2+$\frac{7}{12}$t+1
�ʵ�t=-$\frac{\frac{7}{12}}{2����-\frac{5}{12}��}$=$\frac{7}{10}$ʱ��S���ʱ��G��$\frac{7}{10}$��0��
��3��C1��y=$-\frac{5}{6}$x2+$\frac{13}{6}$x+1��
��C1�ϵĵ㣨x��y���Ƶ�R��3��1����ת180���õ�C2�ϵĶ�Ӧ��Ϊ��x�䣬y�䣩
����$\frac{x+x��}{2}=3$��$\frac{y+y��}{2}=1$��
��ã�x��=6-x��y��=2-x
��C2��2-y=$-\frac{5}{6}$��6-x��2+$\frac{13}{6}$��6-x��+1
�����ã�y=$\frac{5}{6}$x2-$\frac{47}{6}$x+18
��y=0ʱ��0=$\frac{5}{6}$x2-$\frac{47}{6}$x+18����ã�x1=4��x2=$\frac{27}{5}$
S��T������֪����S��4��0��
C1��y=$-\frac{5}{6}$x2+$\frac{13}{6}$x+1�ĶԳ���Ϊ��x=$\frac{13}{10}$��
��K���������Ϊy
��ֱ��SD��y=mx+n���ѵ�S��4��0���͵�D��2��2���������ã�$\left\{\begin{array}{l}{0=4m+n}\\{2=2m+n}\end{array}\right.$����ã�$\left\{\begin{array}{l}{m=-1}\\{n=4}\end{array}\right.$
��ֱ��SD��y=-x+4
��x=$\frac{13}{10}$ʱ��y=2.7����ʱS��D��K��һ��ֱ���ϣ�y��2.7
����G��ƽ����x���ֱ����ֱ��SD�ཻ������ĺ�����Ϊ��x=4-y����x=$\frac{13}{10}$�ľ���Ϊ��4-y-$\frac{13}{10}$
��ͼ4����0��y��2.7ʱ����DSK1�����Ϊ����4-y-$\frac{13}{10}$����2��$\frac{1}{2}$=2.7-y����0��y��2.7��2.7-y��6����������
��y��0ʱ����DSK3�����Ϊ����4-y-$\frac{13}{10}$����[��2-y��-��-y��]��$\frac{1}{2}$=2.7-y����2.7-y��6����ã�y��-3.3����0��y��-3.3ʱ��������
��y��2.7ʱ����DSK2�����Ϊ��[$\frac{13}{10}$-��4-y��]��[y-��y-2��]��$\frac{1}{2}$=y-2.7����y-2.7��6����ã�y��8.7����2.7��y��8.7��������
����������ʹ�á�DSK�����������6ʱ�ĵ�K��������ķ�Χ�ǣ�-3.3��y��8.7����y��2.7��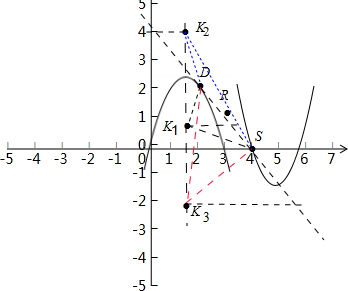
ͼ4
���� ������Ҫ������κ������ۺ������⣬��Ϥ���ε����ʣ����ô���ϵ����������ʱ���ʾ�߶ν�һ����ʾ������꣬��������⽨�����κ��������ֵ�����ǽ���Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5xy��2xyz | B�� | 2��-7 | C�� | -2x2y��5y2z | D�� | 3ac��7bc |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | û��ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | ��������ʵ���� | D�� | ��һ����ʵ������һ����ʵ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4 | B�� | 4 | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | ��2 | D�� | $��\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x}{12}+\frac{x}{16}=1$ | B�� | $\frac{x}{16}+\frac{5+x}{12}=1$ | C�� | 12��5+x��+16x=1 | D�� | 12��5+x��=16x |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com