
分析 (1)方程利用平方根定义开方即可求出解;
(2)原式利用平方根定义,二次根式性质,立方根定义,以及绝对值的代数意义计算即可得到结果;
(3)原式利用二次根式的除法法则计算即可得到结果;
(4)原式利用平方差公式及完全平方公式计算即可得到结果.
解答 解:(1)开方得:x-1=3或x-1=-3,
解得:x1=4,x2=-2;
(2)原式=3-4+2-$\sqrt{2}$+1=2-$\sqrt{2}$;
(3)原式=$\sqrt{\frac{27}{3}}$+$\sqrt{\frac{48}{3}}$=3+4=7;
(4)原式=7-3-4-4$\sqrt{5}$-5=-4$\sqrt{5}$-5.
点评 此题考查了实数的运算,以及解一元二次方程-直接开平方法,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
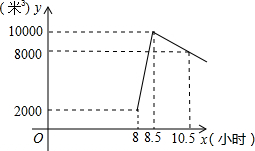 星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.| A. | (1)(2) | B. | (2)(3) | C. | (1)(2)(3) | D. | (1)(2)(3)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com