
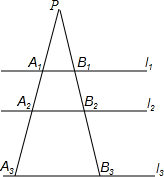
 如图,l1∥l2∥l3,B1B2=$\frac{1}{2}$B2B3,又A1B1=1,A3B3=3,则A2B2=$\frac{5}{3}$,$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{3}{2}$.
如图,l1∥l2∥l3,B1B2=$\frac{1}{2}$B2B3,又A1B1=1,A3B3=3,则A2B2=$\frac{5}{3}$,$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{3}{2}$. 分析 根据l1∥l2∥l3,得到$\frac{{A}_{1}{A}_{2}}{{A}_{2}{A}_{3}}=\frac{{B}_{1}{B}_{2}}{{B}_{2}{B}_{3}}$=$\frac{1}{2}$,设A1A2=k,A1A3=3k,由于$\frac{P{A}_{1}}{P{A}_{3}}$=$\frac{{A}_{1}{B}_{1}}{{A}_{3}{B}_{3}}$=$\frac{1}{3}$,于是得到$\frac{P{A}_{1}}{P{A}_{1}+3k}$=$\frac{1}{3}$,求得PA1=$\frac{3}{2}$k,然后根据$\frac{P{A}_{1}}{P{A}_{2}}$=$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$,
方程求得结论结果.
解答 解:∵l1∥l2∥l3,
∴$\frac{{A}_{1}{A}_{2}}{{A}_{2}{A}_{3}}=\frac{{B}_{1}{B}_{2}}{{B}_{2}{B}_{3}}$=$\frac{1}{2}$,
∴设A1A2=k,A1A3=3k,
∴$\frac{P{A}_{1}}{P{A}_{3}}$=$\frac{{A}_{1}{B}_{1}}{{A}_{3}{B}_{3}}$=$\frac{1}{3}$,
∴$\frac{P{A}_{1}}{P{A}_{1}+3k}$=$\frac{1}{3}$,
∴PA1=$\frac{3}{2}$k,
∴$\frac{P{A}_{1}}{P{A}_{2}}$=$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$,
即:$\frac{\frac{3}{2}k}{\frac{5}{2}k}=\frac{1}{{A}_{2}{B}_{2}}$,
∴A2B2=$\frac{5}{3}$,
∴$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{\frac{3}{2}k}{k}$=$\frac{3}{2}$,
故答案为:$\frac{5}{3}$,$\frac{3}{2}$.
点评 本题考查了平行线分线段成比例,找准对应线段是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
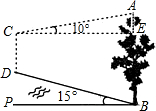 如图,山脚下有一棵树AB,小华从点B沿坡角为15°的坡面上行走50m到达点D,用高为1.5m的测角仪CD测得树顶A的仰角为10°,求树高AB(精确到0.1m)
如图,山脚下有一棵树AB,小华从点B沿坡角为15°的坡面上行走50m到达点D,用高为1.5m的测角仪CD测得树顶A的仰角为10°,求树高AB(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
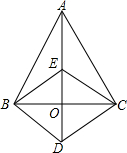 如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE
如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com