练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．抛物线y=4（x-2）2与y轴的交点坐标是（0，16），与x轴的交点坐标为（2，0）．

    分析 根据坐标轴上点的坐标特征，分别计算出自变量为0时的函数值和函数值为0时对应的自变量的值，即可得到该抛物线与坐标轴的交点坐标．

    解答 解：抛物线解析式为y=4（x-2）2，
    当y=0时，4（x-2）2=0，解得x=2，
    所以抛物线与x轴交点坐标为（2，0）；
    当x=0时，y=4（x-2）2=16，
    所以抛物线与y轴交点坐标为（0，16）．
    故答案为：（0，16），（2，0）．

    点评 考查了抛物线与坐标轴的交点问题，了解坐标轴上的点的坐标特点是解答本题的关键，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

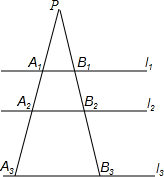    17．如图，l1∥l2∥l3，B1B2=$\frac{1}{2}$B2B3，又A1B1=1，A3B3=3，则A2B2=$\frac{5}{3}$，$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{3}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

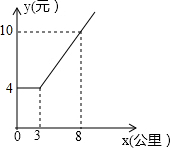    12．某市出租车公司收费标准如图所示，
    （1）求当x＞3时y与x之间的函数关系式．
    （2）如果小明乘此出租车最远能到达13千米处，计算他最多只有多少元钱．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

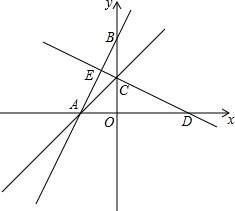    9．如图，在平面直角坐标系中，直线y=2x+4交x轴于点A，交Y轴于点B，点C为BO中点．
    （1）求直线AC的解析式：
    （2）点D在轴正半轴上，直线CD与AB交于点E，若△COD≌△AOB．求
    S△BEC；
    （3）若点M在直线AC上，当S△ABM=2S△AOC时，求点M坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

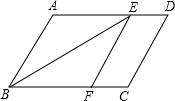    16．如图，在平行四边形ABCD中，∠ABC的平分线交AD于点E，过E作EF∥AB交BC于点F．
    （1）求证：四边形ABFE是菱形；
    （2）若AB=5，BE=8，BC=$\frac{15}{2}$，则菱形ABFE的面积为24，平行四边形ABCD的面积36．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

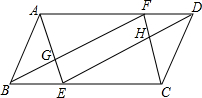    6．如图，在?ABCD中，AB=2，BC=4，∠ABC=60°，E，F分别是BC，AD上的两点，且BE=DF，连AE，BF，DE，CF分别交于点G，H．
    （1）求证：四边形GEHF是平行四边形．
    （2）若E，F分别是BC，AD上的两个动点，设BE=DF=x，试推断当x等于多少时，四边形GEHF是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．某校举办初中生演讲比赛，每班派一名学生参赛，现某班有A、B、C三名学生竞选，他们的笔试成绩和口试成绩（单位：分）分别用两种方式进行了统计，如表和图1：
     ABC
    笔试859590
    口试908085

    （1）请将表和图1中的空缺部分补充完整；
    （2）竞选的最后一个程序是由本校的300名学生代表进行投票，每票计1分，三名候选人的得票情况如图2（没有弃权票，每名学生只能推荐一人），若将笔试、口试、得票三项测试得分按4：3：3的比例确定最后成绩，请计算学生A的最后成绩．

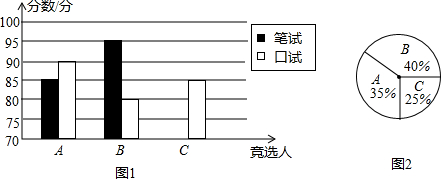
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．在某项针对18-35岁的青年人每天发微信数量的调查中，设一个人的“日均发微信条数”为m，当0≤m＜5时为A级，5≤m＜10时为B级，10≤m＜15时为C级，15≤m＜20时为D级．现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查，根据调查数据整理并制作图表如下：
    青年人日均发微信条数统计表
    m频数百分数
    A级（0≤m＜5）900.3
    B级（5≤m＜10）1200.4
    C级（10≤m＜15）b0.2
    D级（15≤m＜20）30a
    请你根据以上信息解答下列问题：
    （1）在表中：a=0.1，b=60；
    （2）补全频数分布直方图；
    （3）若北京市常住人口中18～35岁的青年人大约有530万人，试估计其中“日均发微信条数”不少于10条的大约有多少万人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

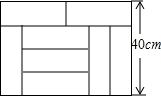    11．如图，用8块相同的长方形地砖拼成一个大长方形，则每个长方形地砖的面积是（　　）
    A．200cm2B．300cm2C．600cm2D．2400cm2

    查看答案和解析>>

    同步练习册答案