
分析 假设x>y>z,则最大的三位数是x×100+y×10+z,最小的三位数是z×100+y×10+x.所以差是(x×100+y×10+z)-(z×100+y×10+x)=99×(x-z),所以原来的三位数是99的倍数,求出可能的取值,进一步解决问题.
解答 解:设x>y>z,则最大的三位数是x×100+y×10+z,最小的三位数是z×100+y×10+x,
所以差是(x×100+y×10+z)-(z×100+y×10+x)=99×(x-z),
所以原来的三位数是99的倍数,可能的取值有198,297,396,495,594,693,792,891,
其中只有495符合要求,954-459=495.
答:这个三位数是495.
故答案为:495.
点评 此题考查了应用类问题,此题也可这样理解:最大三位数,个位最小减去最小三位数的个位时需借位,中间数相同,被借一位后再减,得数只能为9,所以最大数是9;最小数三位数的个位是9,所以相减的个位得数比最小数大1,所以个位就是中间数,得到的三位数,个位是中间数,十位是最大数9,则百位应是最小数;最大三位数百位是9,被借一位,用8减去最小数得到的也是最小数,所以最小数是4;中间数就是5,所以这个数是495.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
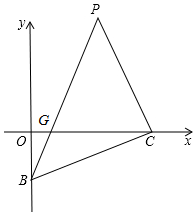 如图,点D(m,n)满足m2-6m+$\sqrt{m+n-6}$=-9,B为y轴负半轴上一动点,∠DBC=45°,BC交x轴于C,CP⊥BC交BD延长线于P,交x轴于点G.
如图,点D(m,n)满足m2-6m+$\sqrt{m+n-6}$=-9,B为y轴负半轴上一动点,∠DBC=45°,BC交x轴于C,CP⊥BC交BD延长线于P,交x轴于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
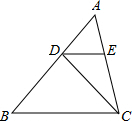 如图,已知在△ABC中,DE∥BC,若AD=2,BD=3.设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,已知在△ABC中,DE∥BC,若AD=2,BD=3.设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在方格纸中,点A,C,D,E,F都在格点上,且直线AC与CD互相垂直.
如图,在方格纸中,点A,C,D,E,F都在格点上,且直线AC与CD互相垂直.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a,b同号,且两数相差1 | |
| B. | a,b异号,且负数的绝对值比正数大1 | |
| C. | a,b同号,且两数和为1 | |
| D. | a,b异号,且正数比负数的绝对值大1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2km/h | B. | 4km/h | C. | 18km/h | D. | 36km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com