
【题目】如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为 . 
【答案】![]()
【解析】解:∵六边形ACDEFG是正六边形,
∴AC=CD,∠ACD=(6﹣2)×180°÷6=120°,
把△ABC和⊙B绕点C旋转120°得△DHC和⊙H,BH的延长线与⊙H的交点为M,
作CN⊥BM于N,如图所示:

则BM的长度就是DB达到的最大值,∠BCH=120°,CH=CB=2,BN=HN,
∴∠B=∠CHB=(180°﹣120°)÷2=30°,
∴CN= ![]() BC=1,
BC=1,
∴BN= ![]() =
= ![]() ,
,
∴BH=2BN=2 ![]() ,
,
∴BM=BH+HM=2 ![]() +1,
+1,
即BD的最大值为2 ![]() +1,
+1,
所以答案是:2 ![]() +1.
+1.
【考点精析】关于本题考查的正多边形和圆,需要了解圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)先化简![]() ,再选一个你喜欢的数求值.
,再选一个你喜欢的数求值.
(1)(﹣2016)0+| ![]() ﹣2|+
﹣2|+ ![]() +3tan30°
+3tan30°
(2)先化简(a2﹣a)÷ ![]() ,再选一个你喜欢的数求值.
,再选一个你喜欢的数求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形OABC的边OC、OA分别在x、y轴的正半轴上,点B坐标为(10,10),点P从O出发沿O→C→B运动,速度为1个单位每秒,连接AP.设运动时间为t.
(1)若抛物线y=﹣(x﹣h)2+k经过A,B两点,求抛物线函数关系式;
(2)当0≤t≤10时,如图1,过点O作OH⊥AP于点H,直线OH交边BC于点D,连接AD,PD,设△APD的面积为S,求S的最小值;
(3)在图2中以A为圆心,OA长为半径作⊙A,当0≤t≤20时,过点P作PQ⊥x轴(Q在P的上方),且线段PQ=t+12:
①当t在什么范围内,线段PQ与⊙A只有一个公共点?当t在什么范围内,线段PQ与⊙A有两个公共点?
②请将①中求得的t的范围作为条件,证明:当t取该范围内任何值时,线段PQ与⊙A总有两个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= , b=;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为;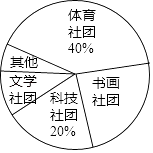
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为﹣1,0,3,点P为数轴上任意点,其对应的数为x.
![]()
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是: ;
(3)如果点P以每分钟2个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了.下面两个图框是用法国“小九九”计算7×8和8×9的两个示例.若用法国的“小九九”计算7×9,左、右手依次伸出手指的个数是( )
|
|
A. 2,3B. 3,3C. 2,4D. 3,4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在市区内,我市乘坐出租车的价格![]() (元)与路程
(元)与路程![]() (km)的函数关系图象如图所示.
(km)的函数关系图象如图所示.

(1)请你根据图象写出两条信息;
(2)小明从学校出发乘坐出租车回家用了13元,求学校离小明家的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com