Question

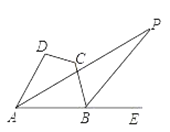
【题目】如图，在四边形ABCD中，∠DAB的角平分线与∠ABC的外角平分线相交于点P，且∠P=20°，∠D=100°，则∠C=______°．

Answer 1

【答案】120

【解析】

利用四边形内角和是360°可以求得∠DAB+∠ABC=360°-∠C-∠D．然后由角平分线的性质及邻补角的定义求得∠PAB+∠ABP=∠DAB+∠ABC+（180°-∠ABC）=90°+（∠DAB+∠ABC），由三角形内角和得∠PAB+∠ABP=180°-∠P，由以上两式可求出∠C的度数．

如图，∵∠DAB+∠ABC+∠C+∠D=360°，

∴∠DAB+∠ABC=360°-∠C-∠D．

又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P，

∴∠PAB+∠ABP=∠DAB+∠ABC+（180°-∠ABC）

=90°+（∠DAB+∠ABC）

=90°+（360°-∠C-∠D）

=270°-∠C-∠D，

∵∠PAB+∠ABP=180°-∠P，

∴270°-∠C-∠D=180°-∠P，

∴270°-∠C-×100°=180°-20°，

∴∠C=120°

故答案为120°.